题目内容
(本题满分12 分)
已知
(Ⅰ)将 化成
化成 的形式;
的形式;
(Ⅱ)求 的最小正周期和最大值以及取得最大值时的
的最小正周期和最大值以及取得最大值时的 的值;
的值;
(Ⅲ)求  的单调递增区间。
的单调递增区间。
(Ⅰ) (Ⅱ)
(Ⅱ) ,
,
(Ⅲ)
解析试题分析:(Ⅰ)



(Ⅱ)因为 所以周期
所以周期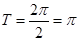 ,
,
当 即
即 时取到最大值
时取到最大值 .
.
(Ⅲ)令 ,解得
,解得 ,所以函数大单调递增区间为
,所以函数大单调递增区间为 .
.
考点:本小题主要考查三角函数的图象和性质,考查性质之前用到两角和与差的正弦、余弦公式和辅助角公式等先化简,考查学生灵活运用公式的能力和数形结合考查图象和性质的能力.
点评:考查三角函数的图象和性质,一定要先把函数化为 或
或 的形式,然后结合三角函数的图象和性质求解.
的形式,然后结合三角函数的图象和性质求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 的最小正周期; 2)求函数
的最小正周期; 2)求函数 上的对称轴方程与零点.
上的对称轴方程与零点. 终边上一点
终边上一点 的坐标为
的坐标为 ,
, ;
; 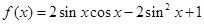
 的最小正周期和值域 (2)求
的最小正周期和值域 (2)求 其中
其中 ,
,
 求
求 的值;(4分)
的值;(4分)  的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,
,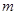 ,使得函数
,使得函数 ,且
,且 满足
满足
 的值.
的值. 的值.
的值. 为第三象限角,
为第三象限角,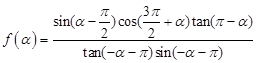 .
. ;
; ,求
,求 ,(
,( )
) 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 时,求
时,求 ,
,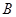 ,
,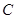 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 , 且
, 且
 是直角三角形;
是直角三角形;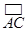 上,
上, ,用
,用 的三角函数表示三角形
的三角函数表示三角形 的面积,并求
的面积,并求