题目内容

在等腰△ABC中，AB=AC=13，BC=10，则此三角形外接圆的半径是（　　）
A、
169
24
B、6
C、12
D、
169
12
分析：通过作辅助线AD⊥BC，可将求△ABC外接圆的半径转化为求Rt△BOD的斜边长．
解答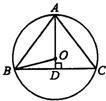：精英家教网解：如图，作AD⊥BC，垂足为D，
所以AD=
132-52
=12；
设OA=r，OB2=OD2+BD2，
即r2=（12-r）2+52，
解得r=
169
24
．
故选A．
点评：此题主要考查等腰三角形外接圆半径的求法，此题综合运用了等腰三角形的三线合一、勾股定理，解题过程中要仔细认真，属于中档题．
练习册系列答案
相关题目
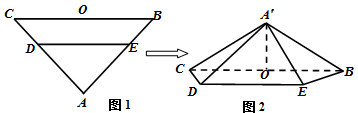
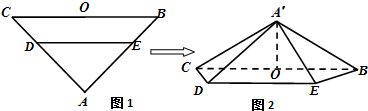如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE，其中A′O=
3
．
（1）证明：A′O⊥平面BCDE；      
（2）求A′D与平面A′BC所成角的正弦值．
如图，在等腰△ABC中，∠A=90°，BC=
2
，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点，求异面直线BE与CD所成角的余弦值．
如图，在等腰△ABC中，AB=AC=1，∠B=30°，则向量
AB
在向量
CA
上的投影等于（　　）
在三角形△ABC中，a，b，c分别是∠A，∠B，∠C的对应边，若asinA=bsinB，则三角形ABC是（　　）
如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE．若A′O⊥平面BCDE，则A′D与平面A′BC所成角的正弦值等于（　　）
精英家教网
A、
2
3
B、
3
3
C、
2
2
D、
2
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网