题目内容
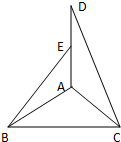 如图,在等腰△ABC中,∠A=90°,BC=
如图,在等腰△ABC中,∠A=90°,BC=| 2 |
分析:由已知可建立如图所示的空间直角坐标系.利用
与
的夹角公式即可得出.
| BE |
| CD |
解答:解:由已知可建立如图所示的空间直角坐标系.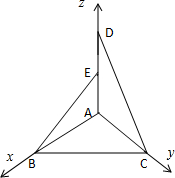
在等腰Rt△ABC中,∵BC=
,∴AB=AC=1.
则A(0,0,0),B(1,0,0),C(0,1,0),D(0,0,1),E(0,0,
).
∴
=(-1,0,
),
=(0,-1,1).
∴cos<
,
>=
=
=
.
∴异面直线BE与CD所成角的余弦值为
.

在等腰Rt△ABC中,∵BC=
| 2 |
则A(0,0,0),B(1,0,0),C(0,1,0),D(0,0,1),E(0,0,
| 1 |
| 2 |
∴
| BE |
| 1 |
| 2 |
| CD |
∴cos<
| BE |
| CD |
| ||||
|
|
| ||||||
|
| ||
| 10 |
∴异面直线BE与CD所成角的余弦值为
| ||
| 10 |
点评:本题考查了考查了通过建立空间直角坐标系利用向量的夹角公式求异面直线所成的角,属于基础题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
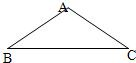 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量| AB |
| AC |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
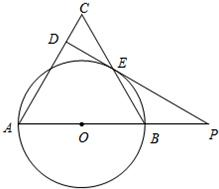 14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由. 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量 如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.