题目内容
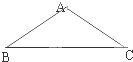 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量| AB |
| CA |
分析:先明确两向量的夹角<
,
>=60?,再得到向量的模,最后用投影的定义求解.
| AB |
| CA |
解答:解:向量
在向量
上的投影为
=|
|?|cos<
,
>|,
因为在等腰△ABC中,AB=AC=1,∠B=30°,所以<
,
>=60?,
所以|
|?|cos<
,
>|=1×cos60?=
,
即向量
在向量
上的投影等于
.
故选A.
| AB |
| CA |
|
| ||||
|
|
| AB |
| AB |
| CA |
因为在等腰△ABC中,AB=AC=1,∠B=30°,所以<
| AB |
| CA |
所以|
| AB |
| AB |
| CA |
| 1 |
| 2 |
即向量
| AB |
| CA |
| 1 |
| 2 |
故选A.
点评:本题主要考查向量投影的概念以及计算,要求熟练掌握向量的投影公式:向量
在向量
上的投影为
=|
|?|cos<
,
>|.
| AB |
| CA |
|
| ||||
|
|
| AB |
| AB |
| CA |

练习册系列答案
相关题目
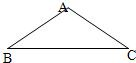 如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量
如图,在等腰△ABC中,AB=AC=1,∠B=30°,则向量| AB |
| AC |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
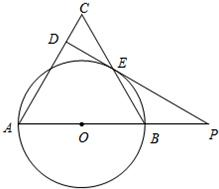 14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
14、如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由. 如图,在等腰△ABC中,
如图,在等腰△ABC中, 如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.
如图,在等腰△ABC中,AC=AB,以AB为直径的⊙O交BC于点E,过点E作⊙O的切线交AC于点D,交AB的延长线于点P.问:PD与AC是否互相垂直?请说明理由.