题目内容
6.在△ABC中,CA=2,CB=6,∠ACB=60°,若点O在∠ACB的平分线上,满足$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,m,n∈R,且-$\frac{1}{2}$≤n≤-$\frac{1}{4}$,则|$\overrightarrow{OC}$|的取值范围是[$\frac{3\sqrt{3}}{4}$,$\sqrt{3}$].分析 根据点O在∠ACB的平分线上,从而可设$\overrightarrow{OC}=k$($\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}+\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$)=$\frac{k}{2}(\overrightarrow{OA}-\overrightarrow{OC})+\frac{k}{6}(\overrightarrow{OB}-\overrightarrow{OC})$,可以求出$\overrightarrow{OC}=\frac{3k}{6+4k}\overrightarrow{OA}+\frac{k}{6+4k}\overrightarrow{OB}$,根据条件,从而有$\frac{k}{6+4k}=n$.根据n的范围,从而得到$-\frac{1}{2}≤\frac{k}{6+4k}≤-\frac{1}{4}$,这样可以解出k的范围,从而可根据${\overrightarrow{OC}}^{2}={k}^{2}(\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}+\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|})^{2}$即可得出${\overrightarrow{OC}}^{2}$的范围,从而得出$|\overrightarrow{OC}|$的范围.
解答 解:∵O在∠ACB的平分线上;
∴存在k,使$\overrightarrow{OC}=k(\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}+\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|})$=$\frac{k}{2}\overrightarrow{CA}+\frac{k}{6}\overrightarrow{CB}$=$\frac{k}{2}(\overrightarrow{OA}-\overrightarrow{OC})+\frac{k}{6}(\overrightarrow{OB}-\overrightarrow{OC})$;
∴$(1+\frac{2k}{3})\overrightarrow{OC}=\frac{k}{2}\overrightarrow{OA}+\frac{k}{6}\overrightarrow{OB}$;
∴$\overrightarrow{OC}=\frac{3k}{6+4k}\overrightarrow{OA}+\frac{k}{6+4k}\overrightarrow{OB}$;
∴$n=\frac{k}{6+4k}$;
∵$-\frac{1}{2}≤n≤-\frac{1}{4}$;
∴$-\frac{1}{2}≤\frac{k}{6+4k}≤-\frac{1}{4}$;
解得$-1≤k≤-\frac{3}{4}$;
${\overrightarrow{OC}}^{2}={k}^{2}(1+2•cos60°+1)=3{k}^{2}$;
$\frac{9}{16}≤{k}^{2}≤1$;
∴$\frac{27}{16}≤{\overrightarrow{OC}}^{2}≤3$;
∴$\frac{3\sqrt{3}}{4}≤|\overrightarrow{OC}|≤\sqrt{3}$;
∴$|\overrightarrow{OC}|$的取值范围是[$\frac{3\sqrt{3}}{4},\sqrt{3}$].
故答案为:[$\frac{3\sqrt{3}}{4},\sqrt{3}$].
点评 考查共线向量基本定理,向量加法的平行四边形法则,菱形的对角线平分对角,向量的数乘运算,向量减法的几何意义,以及平面向量基本定理,向量数量积的运算及计算公式.

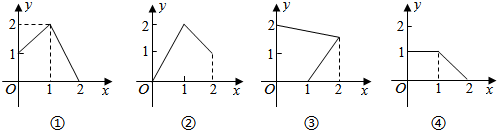
其中能表示从集合M到集合N的函数关系式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 10 | B. | 9 | C. | 6 | D. | 4 |
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.