题目内容
17．函数f（x）=x${\;}^{-\frac{1}{2}}$在区间[1，a]上的最小值是$\frac{\sqrt{2}}{2}$，则a=2．分析 根据幂函数的单调性求出函数的最小值即可．
解答 解：∵f（x）=x${\;}^{-\frac{1}{2}}$在区间[1，a]上为减函数，
∴函数的最小值为f（a）=${a}^{-\frac{1}{2}}=\frac{1}{\sqrt{a}}=\frac{\sqrt{2}}{2}$，
即a=2，
故答案为：2
点评 本题主要考查幂函数的性质，根据幂函数的单调性是解决本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
8．若f（x+$\frac{1}{x}$）=x2+$\frac{1}{{x}^{2}}$+1，则函数f（x）的解析式为（ ）
| A． | f（x）=x2-1 | B． | f（x）=x2-1（x≥2） | ||
| C． | f（x）=x2-1（x≤-2） | D． | f（x）=x2-1（x≥2或x≤-2） |
12．
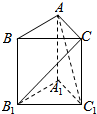如图，在直三棱柱ABC-A1B1C1中，A1B1⊥A1C1，B1C⊥AC1，AB=2，AC=1，则该三棱柱的体积为（ ）
如图，在直三棱柱ABC-A1B1C1中，A1B1⊥A1C1，B1C⊥AC1，AB=2，AC=1，则该三棱柱的体积为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | 4 |