题目内容
2.已知a>1,b>1,且$\frac{1}{a-1}$+$\frac{1}{b-1}$=1,则a+4b的最小值为14.分析 由题意可得a-1>0且b-1>0,可得a+4b=(a-1)+4(b-1)+5=[(a-1)+4(b-1)]($\frac{1}{a-1}$+$\frac{1}{b-1}$)+5=10+$\frac{4(b-1)}{a-1}$+$\frac{a-1}{b-1}$,由基本不等式可得.
解答 解:∵a>1,b>1,
∴a-1>0且b-1>0,
又∵$\frac{1}{a-1}$+$\frac{1}{b-1}$=1,
∴a+4b=(a-1)+4(b-1)+5,
=[(a-1)+4(b-1)]($\frac{1}{a-1}$+$\frac{1}{b-1}$)+5,
=10+$\frac{4(b-1)}{a-1}$+$\frac{a-1}{b-1}$≥10+2$\sqrt{\frac{4(b-1)}{a-1}•\frac{a-1}{b-1}}$=14,
当且仅当$\frac{4(b-1)}{a-1}$=$\frac{a-1}{b-1}$即a=4且b=$\frac{5}{2}$时取等号.
故答案为:14.
点评 本题考查基本不等式求最值,整体法并凑出可用基本不等式的形式是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在锐角△ABC中,已知AB=2,∠B=2∠C,则AC的取值范围是( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{2}$) | C. | (2$\sqrt{2}$,4) | D. | (2,2$\sqrt{3}$) |
11.函数$f(x)=\frac{-3+4x}{5-2x}$的值域是( )
| A. | (-∞,2)∪(2,+∞) | B. | (-∞,-2)∪(-2,+∞) | C. | $({-∞,\frac{5}{2}})∪({\frac{5}{2},+∞})$ | D. | R |
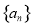 的前
的前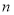 项和
项和 ,且
,且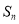 的最大值为8.
的最大值为8.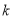 ,并求
,并求 ;
;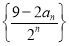 的前
的前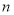 项和
项和 .
.