题目内容
(本小题满分12分)已知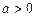 ,设函数
,设函数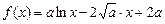 ,
,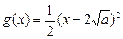 .
.
(Ⅰ)求函数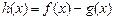 的最大值;
的最大值;
(Ⅱ)若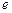 是自然对数的底数,当
是自然对数的底数,当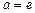 时,是否存在常数
时,是否存在常数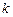 、
、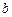 ,使得不等式
,使得不等式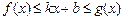 对于任意的正实数
对于任意的正实数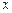 都成立?若存在,求出
都成立?若存在,求出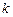 、
、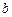 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
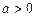 ,设函数
,设函数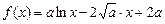 ,
,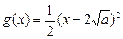 .
.(Ⅰ)求函数
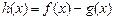 的最大值;
的最大值;(Ⅱ)若
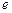 是自然对数的底数,当
是自然对数的底数,当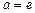 时,是否存在常数
时,是否存在常数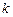 、
、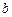 ,使得不等式
,使得不等式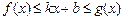 对于任意的正实数
对于任意的正实数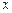 都成立?若存在,求出
都成立?若存在,求出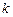 、
、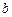 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(本小题满分12分)
解:(I)∵
 , ………………(2分)
, ………………(2分)
∴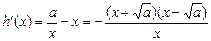 .
.
∴当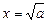 时,函数
时,函数 取最大值
取最大值 ; ………………(4分)
; ………………(4分)
(II)当 时,
时,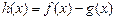 的最大值是0,
的最大值是0,
即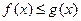 ,当且仅当
,当且仅当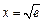 时取等号, ………………(6分)
时取等号, ………………(6分)
函数 和
和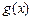 的图象在
的图象在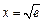 处有且仅有一个公共点
处有且仅有一个公共点 ,
,
∵ ,函数
,函数 的图象在
的图象在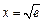 处切线斜率是
处切线斜率是 ,
,
∵ ,函数
,函数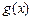 的图象在
的图象在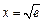 处切线斜率是
处切线斜率是 ,
,
∴ 和
和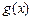 的图象在
的图象在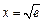 处有公共切线方程为
处有公共切线方程为 ,………………(8分)
,………………(8分)
设 ,
,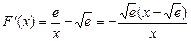
∴当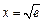 时,函数
时,函数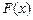 取得最大值
取得最大值 ,∴
,∴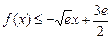 恒成立;……………(10分)
恒成立;……………(10分)
∵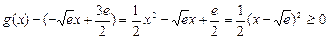 ,
,
∴ 在
在 时恒成立;
时恒成立;
∴当 时,
时, ,
, . ………………(12分)
. ………………(12分)
解:(I)∵

 , ………………(2分)
, ………………(2分)∴
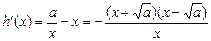 .
.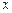 | 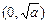 | 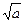 |  |
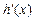 | + | 0 | - |
 |  | 极大值 |  |
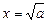 时,函数
时,函数 取最大值
取最大值 ; ………………(4分)
; ………………(4分)(II)当
 时,
时,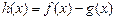 的最大值是0,
的最大值是0,即
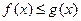 ,当且仅当
,当且仅当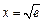 时取等号, ………………(6分)
时取等号, ………………(6分)函数
 和
和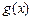 的图象在
的图象在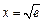 处有且仅有一个公共点
处有且仅有一个公共点 ,
,∵
 ,函数
,函数 的图象在
的图象在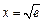 处切线斜率是
处切线斜率是 ,
,∵
 ,函数
,函数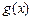 的图象在
的图象在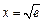 处切线斜率是
处切线斜率是 ,
,∴
 和
和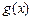 的图象在
的图象在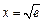 处有公共切线方程为
处有公共切线方程为 ,………………(8分)
,………………(8分)设
 ,
,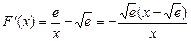
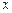 |  |  |  |
 | + | 0 | - |
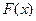 |  | 极大值 |  |
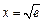 时,函数
时,函数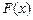 取得最大值
取得最大值 ,∴
,∴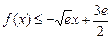 恒成立;……………(10分)
恒成立;……………(10分)∵
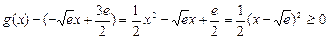 ,
,∴
 在
在 时恒成立;
时恒成立;∴当
 时,
时, ,
, . ………………(12分)
. ………………(12分)略

练习册系列答案
相关题目
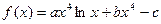 (
(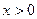 )在
)在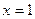 处取得极值
处取得极值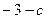 ,其中
,其中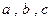 为常数
为常数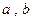 的值; (2)讨论函数
的值; (2)讨论函数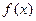 的单调区间
的单调区间 恒成立,求
恒成立,求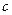 的取值范围
的取值范围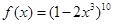 ,则
,则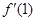 等于
等于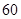
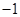
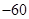
 x3+bx2+cx+bc,
x3+bx2+cx+bc,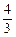 ,试确定b、c的值;
,试确定b、c的值;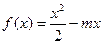 ,其中
,其中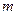 为实常数.
为实常数.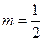 时,求不等式
时,求不等式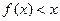 的解集;
的解集;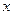 的不等式
的不等式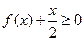 的解集.
的解集.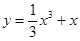 在点
在点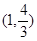 处的切线与坐标轴围成的三角形的面积为( )
处的切线与坐标轴围成的三角形的面积为( )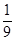
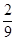
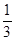
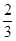


 函数
函数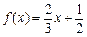 ,
,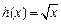 .
.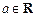 ,解关于x的方程
,解关于x的方程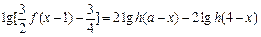 ;
;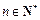 ,证明:
,证明: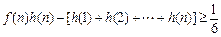 .
.