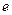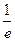题目内容


(1)由 原式得f(x)=x3-ax2-4x+4a,
原式得f(x)=x3-ax2-4x+4a,
∴f′(x)=3 x2-2ax-4.
x2-2ax-4.
由f′(-1)=0得a =,
=,
此时有f(x)=(x2-4),f′(x)=3x2 -x-4.
-x-4.
由f′(x)=0得x=或x=-1,
当x在[-2,2]变化时,f′(x),f(x)的变化如下表:
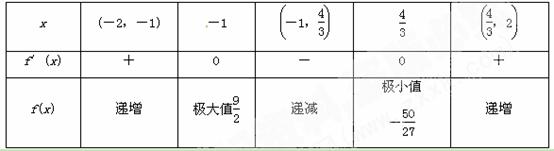 ∵f(x)极小=f=-,f(x)极大=f(-1)=,
∵f(x)极小=f=-,f(x)极大=f(-1)=,
所以f(x)在[-2,2]上的最大值为,最小值为-.
(2)法一:f′(x)=3x2-2ax-4的图象为开口向上且过点(0,-4)的抛物线,由条件得f′(-2)≥0,f′(2)≥0,
即,∴-2≤a≤2.
所以a的取值范围为[-2,2].
 原式得f(x)=x3-ax2-4x+4a,
原式得f(x)=x3-ax2-4x+4a,∴f′(x)=3
 x2-2ax-4.
x2-2ax-4.由f′(-1)=0得a
 =,
=,此时有f(x)=(x2-4),f′(x)=3x2
 -x-4.
-x-4.由f′(x)=0得x=或x=-1,
当x在[-2,2]变化时,f′(x),f(x)的变化如下表:
 ∵f(x)极小=f=-,f(x)极大=f(-1)=,
∵f(x)极小=f=-,f(x)极大=f(-1)=,所以f(x)在[-2,2]上的最大值为,最小值为-.
(2)法一:f′(x)=3x2-2ax-4的图象为开口向上且过点(0,-4)的抛物线,由条件得f′(-2)≥0,f′(2)≥0,
即,∴-2≤a≤2.
所以a的取值范围为[-2,2].
略

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
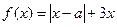 ,其中
,其中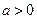 .
.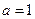 时,求不等式
时,求不等式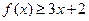 的解集;
的解集;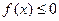 的解集为
的解集为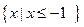 ,求a的值.
,求a的值.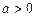 ,设函数
,设函数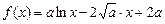 ,
,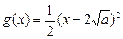 .
.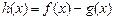 的最大值;
的最大值;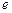 是自然对数的底数,当
是自然对数的底数,当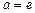 时,是否存在常数
时,是否存在常数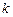 、
、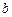 ,使得不等式
,使得不等式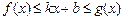 对于任意的正实数
对于任意的正实数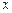 都成立?若存在,求出
都成立?若存在,求出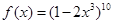 ,则
,则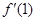 等于
等于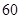
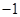
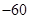
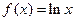
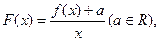 求
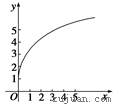
求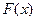 的极值;
的极值;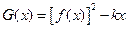 在定义域内单调递减,求满足此条件的实数
在定义域内单调递减,求满足此条件的实数 的取值范围。
的取值范围。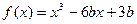 在(0,1)内有极小值,则实数b的取值范围是
在(0,1)内有极小值,则实数b的取值范围是 )
)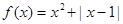 的最小值为
的最小值为 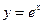 在点A(0,1)处的切线斜率为( )
在点A(0,1)处的切线斜率为( )