题目内容
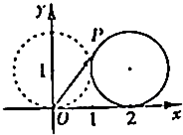 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,| OP |
(2)在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足
|
| ||
|
|
|
| ||
|
|
| AM |
| AN |
分析:(1)由题意点P旋转了2弧度,进而可得P的坐标,即可得向量
的坐标;
(2)建立坐标系,设N(x,1)(0≤x≤2),由题意可得
,
的坐标,进而可得其数量积,可得范围.
| OP |
(2)建立坐标系,设N(x,1)(0≤x≤2),由题意可得
| AN |
| AM |
解答: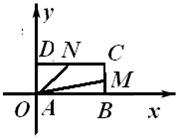 解:(1)根据题意可知圆滚动了2单位个弧长,点P旋转了
解:(1)根据题意可知圆滚动了2单位个弧长,点P旋转了
=2弧度,
此时点P的坐标为:xP=2-cos(2-
)=2-sin2,yP=1+sin(2-
)=1-cos2.
∴
=(2-sin2, 1-cos2).
(2)如图所示,以A为原点,向量
所在直线为x轴,过AD所在直线为y轴建立平面直角坐标系.
∵在矩形ABCD中,AB=2,AD=1,
∴A(0,0),B(2,0),C(2,1),D(0,1).
设N(x,1)(0≤x≤2),则|
|=1,|
|=2-x,|
|=2.
∴由
=
得,|
|=1-
x.
∴M的坐标为(2, 1-
x).
∴
=(x, 1),
=(2, 1-
x).
∴
•
=2x+1-
x=
x+1.
∵0≤x≤2,∴1≤
x+1≤4.
∴
•
的取值范围是[1,4].
故答案为:(2-sin2,1-cos2);[1,4]
 解:(1)根据题意可知圆滚动了2单位个弧长,点P旋转了
解:(1)根据题意可知圆滚动了2单位个弧长,点P旋转了| 2 |
| 1 |
此时点P的坐标为:xP=2-cos(2-
| π |
| 2 |
| π |
| 2 |
∴
| OP |
(2)如图所示,以A为原点,向量
| AB |
∵在矩形ABCD中,AB=2,AD=1,
∴A(0,0),B(2,0),C(2,1),D(0,1).
设N(x,1)(0≤x≤2),则|
| BC |
| CN |
| CD |
∴由
|
| ||
|
|
|
| ||
|
|
| BM |
| 1 |
| 2 |
∴M的坐标为(2, 1-
| 1 |
| 2 |
∴
| AN |
| AM |
| 1 |
| 2 |
∴
| AN |
| AM |
| 1 |
| 2 |
| 3 |
| 2 |
∵0≤x≤2,∴1≤
| 3 |
| 2 |
∴
| AN |
| AM |
故答案为:(2-sin2,1-cos2);[1,4]
点评:本题考查向量的应用,涉及平面向量的数量积的运算,属中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道) 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
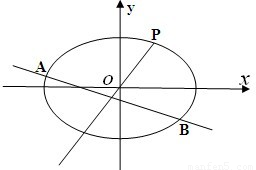
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道) 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆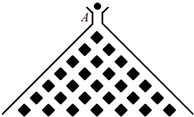 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是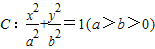 ,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线
,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线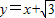 有且只有一个交点.
有且只有一个交点.