题目内容
【题目】已知函数 f(x)=a(|sinx|+|cosx|)﹣sin2x﹣1,a∈R.
(1)写出函数 f(x)的最小正周期(不必写出过程);
(2)求函数 f(x)的最大值;
(3)当a=1时,若函数 f(x)在区间(0,kπ)(k∈N*)上恰有2015个零点,求k的值.
【答案】(1)最小正周期为π.(2)见解析(3)k=1008.
【解析】
(1)由题意结合周期函数的定义直接求解即可;
(2)令![]() ,t∈[1,
,t∈[1,![]() ],则当
],则当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,易知
,易知![]() ,分类比较
,分类比较![]() 、
、![]() 的大小即可得解;
的大小即可得解;
(3)转化条件得当且仅当sin2x=0时,f(x)=0,则x∈(0,π]时,f(x)有且仅有两个零点,结合函数的周期即可得解.
(1)函数 f(x)的最小正周期为π.
(2)∵f(x)=a(|sinx|+|cosx|)﹣sin2x﹣1
=a![]() sin2x﹣1=a
sin2x﹣1=a![]() (sin2x+1),
(sin2x+1),
令t![]() ,t∈[1,
,t∈[1,![]() ],
],
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∵![]() 即
即![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 最大值为
最大值为![]() ;当
;当![]() ,
,![]() 最大值为
最大值为![]() .
.
(3)当a=1时,f(x)![]() ,
,
若f(x)=0,则![]() 即
即![]() ,
,
∴当且仅当sin2x=0时,f(x)=0,
∴x∈(0,π]时,f(x)有且仅有两个零点分别为![]() ,π,
,π,
∴2015=2×1007+1,
∴k=1008.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
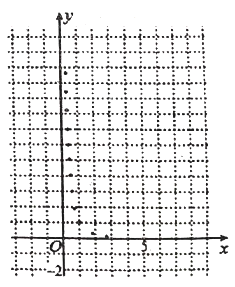
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为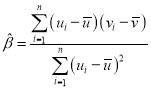 ,
,![]()