题目内容
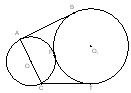
（附加题-选做题）（几何证明选讲）如图，圆O与圆O1外切于点P，一条外公切线分别切两圆于A、B两点，AC为圆O的直径，T为圆O1上任点，CT=AC．求证：CT为圆O1的切线，切点为T．
分析：设圆O的半径为r，圆O1的半径为R（R＞r）过点O1作O1E⊥AC，垂足为E，利用O1E2=AB2=（R+r）2-（R-r）2=4Rr，连接O1C，推出三角形O1CT为直角三角形，即可证明本题．
解答：
证明：设圆O的半径为r，圆O1的半径为R（R＞r）过点O1作O1E⊥AC，垂足
为E，则O1E2=AB2=（R+r）2-（R-r）2=4Rr
连接O1C，则O1C2=O1E2=C1E2=4Rr+（2R-r）2=4R2+r2
因为CT2=AC2=4r2，O1T2=R2
所以O1C2=CT2+O1T2，
所以三角形O1CT为直角三角形，
O1T⊥TC所以CT为圆O1的切线，切点为T
证明：设圆O的半径为r，圆O1的半径为R（R＞r）过点O1作O1E⊥AC，垂足为E，则O1E2=AB2=（R+r）2-（R-r）2=4Rr
连接O1C，则O1C2=O1E2=C1E2=4Rr+（2R-r）2=4R2+r2
因为CT2=AC2=4r2，O1T2=R2
所以O1C2=CT2+O1T2，
所以三角形O1CT为直角三角形，
O1T⊥TC所以CT为圆O1的切线，切点为T
点评：本题是中档题，考查两个圆的位置关系，考查转化思想，计算推理能力，勾股定理的应用．
练习册系列答案
相关题目
附加题 选做题在A、B、C、D四小题中只能选做两小题，每小题10分，共计20分，解答时应写出文字说明、证明过程或演算步骤．