题目内容
将4个相同的白球和5个相同的黑球全部放入3个不同的盒子中，每个盒子既要有白球，
又要有黑球，且每个盒子中球数不能少于2个，则所有不同的放法的种数为（ ）
又要有黑球，且每个盒子中球数不能少于2个，则所有不同的放法的种数为（ ）
| A．12 | B．3 | C．18 | D．6 |
C
分析：本题是一个分步计数问题，首先把四个白球排列，用2块挡板隔开分成3份，共有C32种结果，再把五个黑球用2块挡板分开，共有C42种结果，根据分步计数原理得到结果．
解：由题意知本题是一个分步计数问题，
首先把四个白球排列，用2块挡板隔开分成3份，共有C32=3种结果，
再把五个黑球用2块挡板分开，共有C42=6种结果，
关键分步计数原理知共有3×6=18种结果
故选C．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
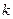次成功，则第
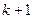次也成功的概率为
，当第
，若首次试验成功和失败的概率都是
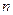次试验成功的概率
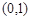上产生两个随机数
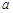和
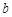，则方程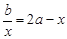
有实根的概率为（ ）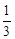
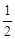
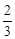
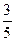，已知比赛中，俄罗斯女排先赢了第一局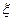，求：
，求
（均用分数作答）.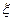
表示摸出的黑球数,写出
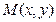的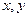
值由掷骰子确定，第一次确定
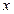，第二次确定
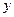，则点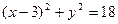
所表示图形的内部（不包括边界）的概率是_________．