题目内容
(06年江西卷理)(12分)
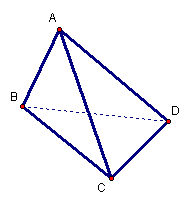
如图,在三棱锥A-BCD中,侧面ABD、ACD
是全等的直角三角形,AD是公共的斜边,
且AD=![]() ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(1)求证:AD^BC
(2)求二面角B-AC-D的大小
(3)在直线AC上是否存在一点E,使ED与面BCD
成30°角?若存在,确定E的位置;若不存在,说明理由。
解析:解法一:
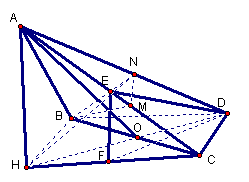
(1)方法一:作AH^面BCD于H,连DH。
AB^BDÞHB^BD,又AD=![]() ,BD=1
,BD=1
\AB=![]() =BC=AC \BD^DC
=BC=AC \BD^DC
又BD=CD,则BHCD是正方形,则DH^BC\AD^BC
方法二:取BC的中点O,连AO、DO
则有AO^BC,DO^BC,\BC^面AOD
\BC^AD
(2)作BM^AC于M,作MN^AC交AD于N,则ÐBMN就是二面角B-AC-D的平面角,因为AB=AC=BC=![]() \M是AC的中点,且MN¤¤CD,则BM=
\M是AC的中点,且MN¤¤CD,则BM=![]() ,MN=
,MN=![]() CD=
CD=![]() ,BN=
,BN=![]() AD=
AD=![]() ,由余弦定理可求得cosÐBMN=
,由余弦定理可求得cosÐBMN=![]()
\ÐBMN=arccos![]()
(3)设E是所求的点,作EF^CH于F,连FD。则EF¤¤AH,\EF^面BCD,ÐEDF就是ED与面BCD所成的角,则ÐEDF=30°。设EF=x,易得AH=HC=1,则CF=x,FD=![]() ,\tanÐEDF=
,\tanÐEDF=![]() =
=![]() =
=![]() 解得x=
解得x=![]() ,则CE=
,则CE=![]() x=1
x=1
故线段AC上存在E点,且CE=1时,ED与面BCD成30°角。
解法二:此题也可用空间向量求解,解答略

练习册系列答案
相关题目



