Question

【题目】有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：

摄氏温度/	－5	0	4	7	12	15	19	23	27	31	36
热饮杯数	156	150	132	128	130	116	104	89	93	76	54

(1)画出散点图；

(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律；

(3)求回归方程；

(4)如果某天的气温是，预测这天卖出的热饮杯数．

Answer 1

【答案】（1）解析见散点图；（2）气温与热饮销售杯数之间呈负相关，即气温越高，卖出去的热饮杯数越少；（3） ；（4）.

【解析】试题分析：（1）根据数据，画出散点图；（2）观察得到气温与热饮销售杯数之间呈负相关，即气温越高，卖出去的热饮杯数越少；（3）利用回归方程的公式求出回归系数,，得到回归方程；（4）当x＝2时， ＝143.063.因此，某天的气温为2 ℃时，这天大约可以卖出143杯热饮．

试题解析：

(1)散点图如图所示：

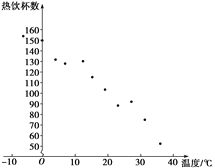
(2)从上图看到，各点散布在从左上角到右下角的区域里，因此，气温与热饮销售杯数之间呈负相关，即气温越高，卖出去的热饮杯数越少．

(3)从散点图可以看出，这些点大致分布在一条直线的附近，因此，可用公式求出回归方程的系数．利用计算器容易求得回归方程＝－2.352x＋147.767.

(4)当x＝2时， ＝143.063.因此，某天的气温为2 ℃时，这天大约可以卖出143杯热饮．