题目内容
13.已知sin(α-$\frac{π}{6}$)=$\frac{3}{5}$,α∈(0,$\frac{π}{2}$),求sin(2α+$\frac{π}{6}$)的值.分析 解:根据同角三角函数关系式结合角的范围可求cos(α-$\frac{π}{6}$),由倍角公式可求得sin(2α-$\frac{π}{3}$),从而根据sin(2α+$\frac{π}{6}$)=sin(2α-$\frac{π}{3}$+$\frac{π}{2}$)=cos(2α-$\frac{π}{3}$)即可求值.
解答 解:∵α∈(0,$\frac{π}{2}$),sin(α-$\frac{π}{6}$)=$\frac{3}{5}$,
∴α-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{π}{3}$),2α-$\frac{π}{3}$∈(0,$\frac{2π}{3}$),
∴cos(α-$\frac{π}{6}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{6})}$=$\frac{4}{5}$,sin2(α-$\frac{π}{6}$)=sin(2α-$\frac{π}{3}$)=2sin(α-$\frac{π}{6}$)cos(α-$\frac{π}{6}$)=2×$\frac{3}{5}$×$\frac{4}{5}$=$\frac{24}{25}$,
∴sin(2α+$\frac{π}{6}$)=sin(2α-$\frac{π}{3}$+$\frac{π}{2}$)=cos(2α-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}(2α-\frac{π}{3})}$=$\frac{7}{25}$.
点评 本题主要考查了同角三角函数关系式,诱导公式,倍角公式的综合应用,解题时注意分析角的范围,属于基本知识是考查.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
3.己知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是( )
| A. | -3∈A | B. | 3∉B | C. | A∪B=B | D. | A∩B=B |
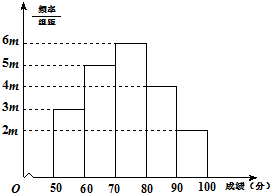 有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示: