题目内容
18.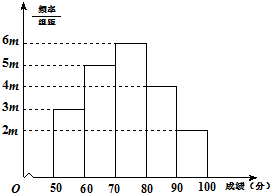 有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:(I)求频率分布直方图中m的值;
(Ⅱ) 分别求出成绩落在[70,80),[80,90),[90,100]中的学生人数;
(Ⅲ)从成绩在[80,100]的学生中任选2人,求所选学生的成绩都落在[80,90)中的概率.
分析 (Ⅰ)根据各小组频率和等于1,求出m的值;
(Ⅱ)利用频率=$\frac{频数}{样本容量}$,计算成绩落在[70,80)、[80,90)、[90,100]中的学生人数;
(Ⅲ)用列举法求出从[80,100]中的学生抽取2人的基本事件数以及此2人的成绩都在[80,90)的基本事件数,求出概率即可.
解答 解:(Ⅰ)根据各小组频率和等于1,得;
10×(2m+3m+4m+5m+6m)=1,
∴m=0.005;
(Ⅱ)成绩落在[70,80)中的学生人数为
20×10×0.03=6,
成绩落在[80,90)中的学生人数是
20×10×0.02=4,
成绩落在[90,100]中的学生人数2是
0×10×0.01=2;
(Ⅲ)设落在[80,90)中的学生为a1,a2,a3,a4,
落在[90,100]中的学生为b1,b2,则
Ω1={a1a2,a1a3,a1a4,a1b1,a1b2,a2a3,a2a4,a2b1,a2b2,a3a4,a3b1,a3b2,a4b1,a4b2,b1b2},
基本事件个数为n=15,
设A=“此2人的成绩都在[80,90)”,则事件A包含的基本事件数m=6,
∴事件A发生的概率为P(A)=$\frac{m}{n}=\frac{6}{15}=\frac{2}{5}$.
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
9.设f0(x)=|x|-10,fn(x)=|fn-1(x)|-1(n∈N*),则函数y=f20(x)的零点个数为( )
| A. | 19 | B. | 20 | C. | 31 | D. | 22 |
6.已知a,b,c分别是△内角A,B,C的对边,且(b-c)(sinB+sinC)=(a-$\sqrt{3}c$)•sinA,则角B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
3.现有12张不同的卡片,其中红色、黄色、绿色、蓝色卡片各3张,从中任取3张,要求这3张卡片不能是同一种颜色,且蓝色卡片至多1张.则不同的取法的共有( )
| A. | 135 | B. | 172 | C. | 189 | D. | 216 |
10.已知二次函数y=$\frac{{x}^{2}}{4}$和直线y=kx+1交于A、B两点,∠AOB=120°,则S△AOB=( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |
8.某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的2×2列联表,
(1)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 50 | 60 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 80 | 110 |
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式与临界值表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |