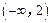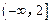题目内容
已知圆的方程为x2+ y2-6x-8y=0,设圆中过点(2,5)的最长弦与最短弦分别为AB、CD,则直线AB与CD的斜率之和为
A.-1 B.0 C.1 D.-2
A.-1 B.0 C.1 D.-2
B
专题:计算题.
分析:把圆的方程化为标准方程,找出圆心坐标,由(2,5)在圆内,故过此点最长的弦为直径,最短弦为与这条直径垂直的弦,所以由圆心坐标和(2,5)求出直线AB的斜率,再根据两直线垂直时斜率的乘积为-1求出直线CD的斜率,进而求出两直线的斜率和.
解答:解:把圆的方程化为标准方程得:(x-3)2+(y-4)2=25,
∴圆心坐标为(3,4),
∴过(2,5)的最长弦AB所在直线的斜率为
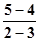 =-1,
=-1,又最长弦所在的直线与最短弦所在的直线垂直,
∴过(2,5)最短弦CD所在的直线斜率为1,
则直线AB与CD的斜率之和为-1+1=0.
故选B
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,垂径定理,直线斜率的计算方法,以及两直线垂直时斜率满足的关系,其中得出过点(2,5)最长的弦为直径,最短弦为与这条直径垂直的弦是解本题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 内有一点P(-1,2),AB为过点p且倾斜角为
内有一点P(-1,2),AB为过点p且倾斜角为 的弦,
的弦, 时,求AB的长;
时,求AB的长; 上,与
上,与 轴相切,且被直线
轴相切,且被直线 截得弦长为
截得弦长为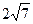 的圆的方程
的圆的方程 .
. ,且直线l与x轴交点
,且直线l与x轴交点 ,圆
,圆 与x轴交
与x轴交 两点.
两点. 交圆于
交圆于 两点,且圆孤
两点,且圆孤 恰为圆周的
恰为圆周的 ,求直线
,求直线 (3)过M点作直线
(3)过M点作直线 与圆相切于点
与圆相切于点 ,设(2)中椭圆的两个焦点分别为
,设(2)中椭圆的两个焦点分别为 ,求三角形
,求三角形 面积.
面积.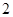 ,圆心在
,圆心在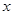 轴的正半轴上,直线
轴的正半轴上,直线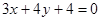 与圆C相切,则圆C的方程为 ( ■ )
与圆C相切,则圆C的方程为 ( ■ )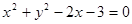
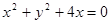
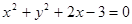
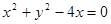
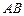 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径, 是⊙O与l的公共点,
是⊙O与l的公共点,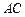 ⊥l,
⊥l,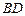 ⊥l,垂足分别为
⊥l,垂足分别为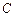 ,
,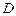 ,且
,且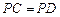 ,
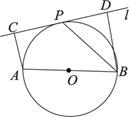
,
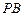 平分∠ABD.
平分∠ABD.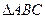 中,
中,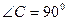 ,BE是
,BE是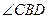 角平分线,
角平分线,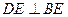 交AB于D,
交AB于D,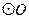 是
是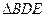 的外接圆。
的外接圆。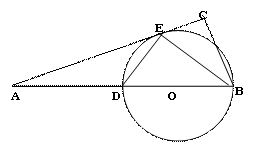
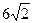 ,求BC的长。
,求BC的长。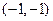 ,B(
,B(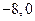 ), C(0,6)的圆的方程,并指出这个圆半径和圆心坐标.
), C(0,6)的圆的方程,并指出这个圆半径和圆心坐标.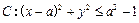 的面积为
的面积为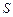 ,平面区域
,平面区域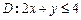 与圆面
与圆面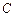 的公共区域的面积大于
的公共区域的面积大于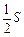 ,则实数
,则实数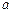 的取值范围是
的取值范围是