题目内容
3.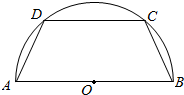 如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.(1)写出这个梯形周长y与腰长x间的函数关系式,并求出它的定义域;
(2)求这个梯形周长的最大值及此时的腰长.
分析 (1)连接OD,OC,在△OAD中,若设∠AOD=θ,由余弦定理可得,cosθ=$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$;在△OCD中,由∠COD=180°-2θ,可得DC2=2R2-2R2•cos(180°-2θ),从而得DC;即得梯形的周长y和x的取值范围.
(2)利用配方法,可得这个梯形周长的最大值及此时的腰长.
解答 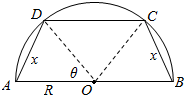 解:(1)如图所示,连接OD,OC,则OC=OD=OA=OB=R,
解:(1)如图所示,连接OD,OC,则OC=OD=OA=OB=R,
在△OAD中,设∠AOD=θ,AD=x,由余弦定理,得
x2=2R2-2R2•cosθ,θ∈(0,90°),∴cosθ=$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$;
在△OCD中,∠COD=180°-2θ,同理:
DC2=2R2-2R2•cos(180°-2θ)=2R2(1+cos2θ)=2R2•2cos2θ=4R2•cos2θ,
∴DC=2R•cosθ=2R•$\frac{2{R}^{2}-{x}^{2}}{2{R}^{2}}$=2R-$\frac{{x}^{2}}{R}$;
所以梯形的周长:y=2R+2x+(2R-$\frac{{x}^{2}}{R}$)=-$\frac{{x}^{2}}{R}$+2x+4R;
∵x2=2R2-2R2•cosθ<2R2,∴x<$\sqrt{2}$R,∴定义域为(0,$\sqrt{2}$R).
(2)y=-$\frac{{x}^{2}}{R}$+2x+4R=-$\frac{1}{R}$(x-R)2+5R,∴x=R,梯形周长的最大值5R.
点评 本题考查了余弦定理在解三角形中的应用,也考查了二倍角公式的灵活应用,考查配方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某商店销售一种商品,要以不低于超过进价20%价格才能出售,但为了获得更多利润,该店以高出进价80%的价格标价.若顾客想买下标价为360元的这种商品,商店最多可以降价( )
| A. | 240元 | B. | 160元 | C. | 120元 | D. | 100元 |