题目内容
13.若三条直线4x+y+4=0,mx+y+1=0,x-y+1=0不能围成三角形,则实数m取值范围是{4,1,-1}.分析 三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x-y+1=0不能围成三角形,可得l2∥l1或l2∥l3或l2经过直线l1与l3的交点,解出即可.
解答 解:由题意,联立$\left\{\begin{array}{l}{4x+y+4=0}\\{x-y+1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴直线l1与l3的交点为(-1,0);
∵三条直线l1:4x+y+4=0,l2:mx+y+1=0,l3:x-y+1=0不能围成三角形,
∴l2∥l1或l2∥l3或l2经过直线l1与l3的交点,
即-m=-4,或-m=1,或-m+0+1=0,
解得m=4,或m=±1.
故答案为:{4,1,-1}.
点评 本题考查了相互平行的直线斜率之间的关系、三角形的性质,属于基础题目.

练习册系列答案
相关题目
3.方程x3-3x+c=0恰有两个实数根,则c=( )
| A. | -2或2 | B. | -9或3 | C. | -1或1 | D. | -3或1 |
8.函数f(x)=$\frac{{{x^2}-2x+3}}{x}$(x<0),取得最大值为( )
| A. | -2$\sqrt{3}$-2 | B. | 2-2$\sqrt{3}$ | C. | 2$\sqrt{3}$-2 | D. | 2$\sqrt{3}$+2 |
18.两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求?
| 机床甲 | 10 | 9.8 | 10 | 10.2 |
| 机床乙 | 10.1 | 10 | 9.9 | 10 |
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),(x>0)}\\{{3}^{-x},(x≤0)}\end{array}\right.$,若f(m)>1,则实数m的取值范围是( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,1)∪(3,+∞) |
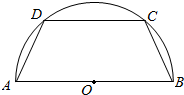 如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.