题目内容
8.某商店销售一种商品,要以不低于超过进价20%价格才能出售,但为了获得更多利润,该店以高出进价80%的价格标价.若顾客想买下标价为360元的这种商品,商店最多可以降价( )| A. | 240元 | B. | 160元 | C. | 120元 | D. | 100元 |
分析 设这件商品的进价为x,根据题意可得高出进价80%的价格标价为360元,列出方程,求出x的值,然后再求出最低出售价,用标价-最低出售价即可求得结论.
解答 解:设这件商品的进价为x.
据题意可得:(1+80%)•x=360,
解得:x=200.
盈利的最低价格为200×(1+20%)=240,
∴商店老板最多会降价360-240=120(元).
故选:C.
点评 本题考查一元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
18.两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求?
| 机床甲 | 10 | 9.8 | 10 | 10.2 |
| 机床乙 | 10.1 | 10 | 9.9 | 10 |
13.给定函数:①y=x2②y=($\frac{1}{2}$)x+1③y=log2|x|④y=|log2x|,其中在区间(0,1)上满足“当x1<x2”时,都有f(x1)>f(x2)的函数序号是( )
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
20.下列函数中,在(0,2)上为增函数的是( )
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=log2(x-1) | C. | y=log2$\frac{1}{x}$ | D. | y=log2|x| |
17.设偶函数f(x)对任意x∈R都有f(x)=-$\frac{1}{f(x-3)}$,且当x∈[-3,-2]时,f(x)=4x,则f(5.5)=( )
| A. | 10 | B. | -10 | C. | $\frac{1}{10}$ | D. | -$\frac{1}{10}$ |
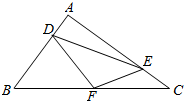 在△ABC中,AB⊥AC,AB=3,AC=4,D,E分别是边AB,AC上的点,且AD=CE=x,设四边形BDEC的面积为S,周长为c.
在△ABC中,AB⊥AC,AB=3,AC=4,D,E分别是边AB,AC上的点,且AD=CE=x,设四边形BDEC的面积为S,周长为c.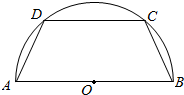 如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图所示,有一半径为R的半圆形钢板,计划剪裁成一等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.