分别与两条异面直线平行的两条直线的位置关系为异面或相交．题目和参考答案——青夏教育精英家教网——

题目内容

14．分别与两条异面直线平行的两条直线的位置关系为异面或相交．

分析根据空间两条直线的位置关系分别判断即可．

解答解：在空间中分别和两条异面直线平行的两条直线的位置关系异面或相交．
故答案为：异面或相交．

点评本题主要考查空间异面直线的性质和空间两直线的位置关系的判断，比较基础．

练习册系列答案

中考备考每天一点系列答案

征服英语名师课时计划系列答案

考前系列答案

口算心算快速算系列答案

跨越中考总复习方略系列答案

新语文阅读训练系列答案

秒杀口算题系列答案

口算题卡加应用题集训系列答案

中考1加1系列答案

鼎尖阅读系列答案

相关题目

4．如果a＞b，c＞d，是否一定能够得出ac＞bd？并说明理由．

5．计算：
（1）（1.5）^-2+（-9.6）⁰-（3$\frac{3}{8}$）^-${\;}^{\frac{2}{3}}$+$\sqrt{（π-4）^{2}}$；
（2）lg16+3lg5-lg$\frac{1}{5}$．

2．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x+1），（x＞0）}\\{{3}^{-x}，（x≤0）}\end{array}\right.$，若f（m）＞1，则实数m的取值范围是（　　）

（-∞，0）∪（2，+∞）

（-∞，1）∪（3，+∞）

9．a∥α、b∥α、则a与b（　　）

以上均有可能

19．若函数f（x）是奇函数，当x＞0时，f（x）=x-x²，则当x＜0时，f（x）=x²+x．

6．命题“?x∈[1，2]，x²+ax+9≥0”是假命题，则实数a的取值范围是（-∞，-$\frac{13}{2}$）．

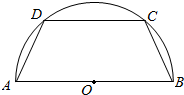如图所示，有一半径为R的半圆形钢板，计划剪裁成一等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．
（1）写出这个梯形周长y与腰长x间的函数关系式，并求出它的定义域；
（2）求这个梯形周长的最大值及此时的腰长．

4．已知函数f（x）=log₂（x²+2x-3），则函数f（1nx）的定义域是（　　）

（-∞，e^-3]∪[e，+∞）

（0，e^-3）∪（e，+∞）