题目内容
已知函数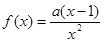 ,其中
,其中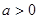 .
.
(Ⅰ)求函数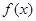 的单调区间;
的单调区间;
(Ⅱ)若直线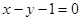 是曲线
是曲线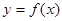 的切线,求实数
的切线,求实数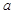 的值;
的值;
(Ⅲ)设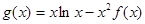 ,求
,求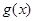 在区间
在区间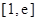 上的最小值.(
上的最小值.(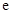 为自然对数的底数)
为自然对数的底数)
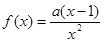 ,其中
,其中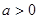 .
.(Ⅰ)求函数
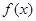 的单调区间;
的单调区间;(Ⅱ)若直线
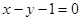 是曲线
是曲线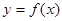 的切线,求实数
的切线,求实数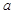 的值;
的值;(Ⅲ)设
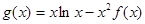 ,求
,求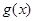 在区间
在区间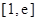 上的最小值.(
上的最小值.(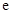 为自然对数的底数)
为自然对数的底数)(Ⅰ)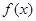 的单调递减区间是
的单调递减区间是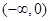 和
和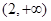 ,单调递增区间是
,单调递增区间是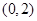 ;(Ⅱ)
;(Ⅱ)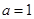 ;
;
(Ⅲ)当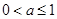 时,
时,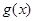 最小值为
最小值为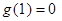 ;当
;当 时,
时,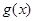 的最小值
的最小值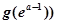 =
= ;当
;当 时,
时,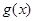 最小值为
最小值为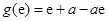 .
.
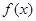 的单调递减区间是
的单调递减区间是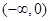 和
和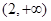 ,单调递增区间是
,单调递增区间是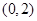 ;(Ⅱ)
;(Ⅱ)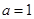 ;
;(Ⅲ)当
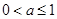 时,
时,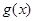 最小值为
最小值为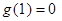 ;当
;当 时,
时,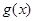 的最小值
的最小值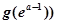 =
= ;当
;当 时,
时,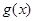 最小值为
最小值为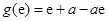 .
.试题分析:(Ⅰ)根据函数求解导数,然后令导数大于零或者小于零得到单调区间;
(Ⅱ)根据给定的切线方程得到切点的坐标,进而得到参数的值;
(Ⅲ)对于函数的最值问题,根据给定的函数,求解导数,运用导数的符号判定单调性,和定义域结合得到最值.
试题解析:(Ⅰ)
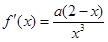 ,(
,( ), 2分
), 2分在区间
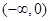 和
和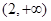 上,
上,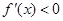 ;在区间
;在区间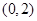 上,
上,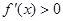 .
.所以,
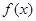 的单调递减区间是
的单调递减区间是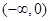 和
和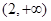 ,单调递增区间是
,单调递增区间是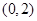 . 4分
. 4分(Ⅱ)设切点坐标为
 ,则
,则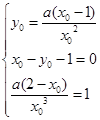 6分(1个方程1分)
6分(1个方程1分)解得
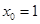 ,
,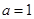 . 7分
. 7分(Ⅲ)
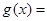
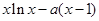 ,
,则
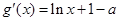 , 8分
, 8分解
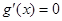 ,得
,得 ,
,所以,在区间
 上,
上,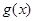 为递减函数,
为递减函数,在区间
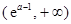 上,
上,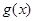 为递增函数. 9分
为递增函数. 9分当
 ,即
,即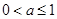 时,在区间
时,在区间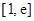 上,
上,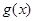 为递增函数,
为递增函数,所以
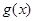 最小值为
最小值为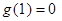 . 10分
. 10分当
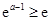 ,即
,即 时,在区间
时,在区间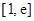 上,
上,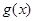 为递减函数,
为递减函数,所以
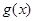 最小值为
最小值为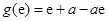 . 11分
. 11分当
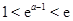 ,即
,即 时,最小值
时,最小值 =
= .
. 综上所述,当
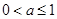 时,
时,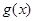 最小值为
最小值为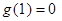 ;当
;当 时,
时,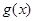 的最小值
的最小值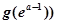 =
= ;当
;当 时,
时,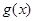 最小值为
最小值为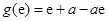 . 12分
. 12分
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
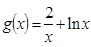 ,
,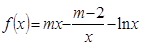 ,
,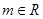 .
.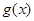 的极值点;
的极值点;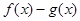 在
在 上为单调函数,求
上为单调函数,求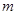 的取值范围;
的取值范围; ,若在
,若在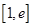 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求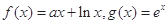 .
.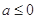 时,求
时,求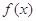 的单调区间
的单调区间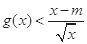 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;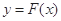 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数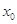 ,称
,称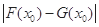 的值为两函数在
的值为两函数在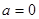 时,函数
时,函数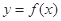 和
和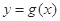 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。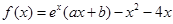 ,曲线
,曲线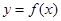 在点
在点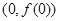 处切线方程为
处切线方程为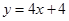 .
.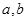 的值;
的值;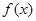 的单调性,并求
的单调性,并求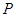 元,则销售量
元,则销售量 (单位:件)与零售价
(单位:件)与零售价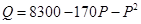 ,问该商品零售价定为多少元时毛利润
,问该商品零售价定为多少元时毛利润 最大,并求出最大毛利润.(毛利润
最大,并求出最大毛利润.(毛利润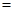 销售收入
销售收入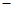 进货支出)
进货支出)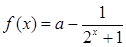 .
.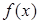 存在零点,求
存在零点,求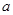 的取值范围
的取值范围 ,使
,使 为奇函数?如果存在,求
为奇函数?如果存在,求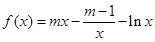 ,
,  在
在 上为增函数,且
上为增函数,且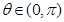 ,求解下列各题:
,求解下列各题: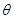 的取值范围;
的取值范围; 在
在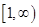 上为单调增函数,求
上为单调增函数,求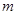 的取值范围;
的取值范围; ,若在
,若在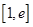 上至少存在一个
上至少存在一个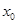 ,使得
,使得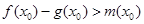 成立,求
成立,求 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数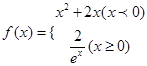 ,则
,则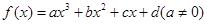 的对称中心为
的对称中心为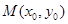 ,记函数
,记函数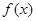 的导函数为
的导函数为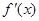 ,
,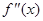 ,则有
,则有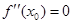 .若函数
.若函数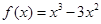 ,则可求得
,则可求得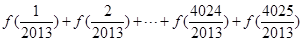 _________.
_________.