题目内容
已知函数f(x)=2ax-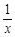 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0)
(Ⅰ)当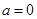 时,求
时,求 的极值;
的极值;
(Ⅱ)当a>0时,讨论 的单调性;
的单调性;
(Ⅲ)若对任意的a∈(2,3),x1,x2∈[1,3],恒有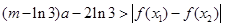 成立,求实数m的取值范围。
成立,求实数m的取值范围。
(Ⅰ) 的极大值为
的极大值为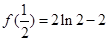 ,无极小值;(Ⅱ)①当
,无极小值;(Ⅱ)①当 时,
时, 在
在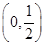 和
和 上是增函数,在
上是增函数,在 上是减函数;②当
上是减函数;②当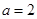 时,
时, 在
在 上是增函数;③当
上是增函数;③当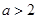 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 ; (Ⅲ)
上是减函数 ; (Ⅲ)
解析试题分析:(Ⅰ)当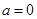 时,求
时,求 的极值,首先确定函数的定义域为
的极值,首先确定函数的定义域为 ,对函数
,对函数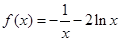 求导函数
求导函数 ,确定函数的单调性,即可求得函数
,确定函数的单调性,即可求得函数 的极值;(Ⅱ)当a>0时,讨论
的极值;(Ⅱ)当a>0时,讨论 的单调性,首先对函数
的单调性,首先对函数 求导函数
求导函数 ,并分解得
,并分解得 ,再进行分类讨论,利用
,再进行分类讨论,利用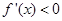 ,确定函数单调减区间;
,确定函数单调减区间; ,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有
,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有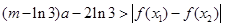 成立,只要求出
成立,只要求出 的最大值即可,因此确定函数
的最大值即可,因此确定函数 在
在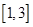 上单调递减,可得
上单调递减,可得 的最大值与最小值,从而得
的最大值与最小值,从而得 ,进而利用分离参数法,可得
,进而利用分离参数法,可得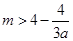 ,从而可求实数
,从而可求实数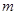 的取值范围
的取值范围
试题解析:(Ⅰ)当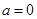 时,
时,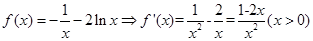 2分
2分
由 ,解得
,解得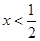 ,可知
,可知 在
在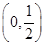 上是增函数,在
上是增函数,在 上是减函数 4分
上是减函数 4分
∴ 的极大值为
的极大值为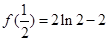 ,无极小值 5分
,无极小值 5分
(Ⅱ)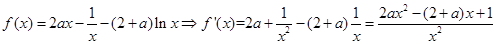 ,
,
①当 时,
时, 在
在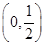 和
和 上是增函数,在
上是增函数,在 上是减函数; 7分
上是减函数; 7分
②当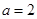 时,
时, 在
在 上是增函数; 8分
上是增函数; 8分
③当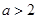 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 9分
上是减函数 9分
(Ⅲ)当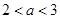 时,由(2)可知
时,由(2)可知 在
在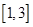 上是增函数,
上是增函数,
∴ 10分
10分
由 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
∴ 11分
11分
即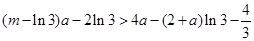 对任意
对任意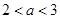 恒成立,
恒成立,
即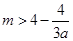 对任意
对任意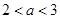 恒成立, 12分
恒成立, 12分
由于当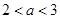 时,
时, ,∴
,∴ 14分
14分
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性;函数在某点取得极值的条件

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案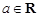 ,函数
,函数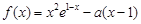 .
.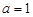 时,求
时,求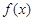 在
在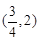 内的极大值;
内的极大值;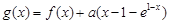 ,当
,当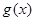 有两个极值点
有两个极值点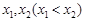 时,总有
时,总有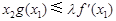 ,求实数
,求实数 的值.(其中
的值.(其中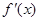 是
是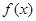 的导函数.)
的导函数.)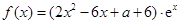 (
(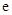 为自然对数的底数).
为自然对数的底数).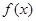 在
在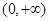 上的单调区间;
上的单调区间;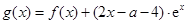 ,是否存在区间
,是否存在区间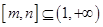 ,使得当
,使得当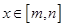 时函数
时函数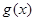 的值域为
的值域为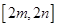 ,若存在求出
,若存在求出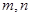 ,若不存在说明理由.
,若不存在说明理由. 。
。 的极值点;
的极值点; 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围; 时,
时, 。
。 ,
,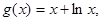 其中
其中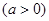
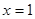 是函数
是函数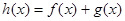 的极值点,求实数
的极值点,求实数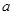 的值;
的值;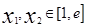 (
(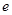 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数
 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0. 的解析式;
的解析式;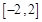 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ,求实数
,求实数 的最小值;
的最小值;
 ,可作曲线
,可作曲线 的三条切线,求实数
的三条切线,求实数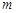 的取值范围.
的取值范围.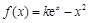 (其中
(其中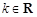 ,e是自然对数的底数).
,e是自然对数的底数).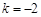 ,试判断函数
,试判断函数 在区间
在区间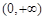 上的单调性;
上的单调性;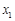 ,
,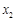 (
(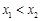 ),求k的取值范围;
),求k的取值范围;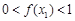 .
.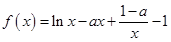 .
.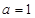 时,求曲线
时,求曲线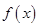 在
在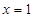 处的切线方程;
处的切线方程;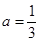 时,求函数
时,求函数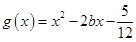 ,若对于
,若对于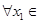 [1,2],
[1,2],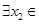 [0,1],使
[0,1],使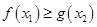 成立,求实数
成立,求实数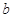 的取值范围.
的取值范围.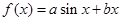 的图像在点
的图像在点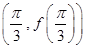 处的切线方程为
处的切线方程为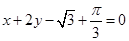 .
. ,
,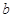 的值;
的值;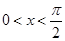 时,
时,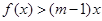 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.