题目内容
 已知定义在区间[-π,
已知定义在区间[-π,| 3π |
| 2 |
| π |
| 4 |
| π |
| 4 |
(1)作出y=f(x)的图象;
(2)求y=f(x)的解析式;
(3)若关于x的方程f(x)=-
| 9 |
| 10 |
分析:(1)根据图象的对称性做出y=f(x)的图象.
(2)任取x∈[-π,
],则
-x∈[
,
],由题意得f(x)=f(
-x).再根据当x≥
时,f(x)=-sinx,
求出解析式.
(3)因为-
∈(-1,-
),f(x)=-
有4个根满足 x1<x2<
<x3<x4,利用对称性求出M的值.
(2)任取x∈[-π,
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 4 |
求出解析式.
(3)因为-
| 9 |
| 10 |
| ||
| 2 |
| 9 |
| 10 |
| π |
| 4 |
解答:解:(1)y=f(x)的图象如图所示.
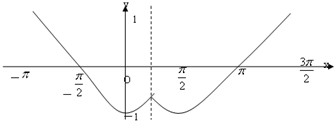 (.4分)
(.4分)
(2)任取x∈[-π,
],则
-x∈[
,
],由于函数f(x)图象关于直线x=
对称,
则f(x)=f(
-x).(6分)
又当x≥
时,f(x)=-sinx,则f(x)=f(
-x)=-sin(
-x)=-cosx,(8分)
即f(x)=
.(10分)
(3)因为-
∈(-1,-
),f(x)=-
有4个根满足 x1<x2<
<x3<x4,(12分)
由对称性得,x1+x2=0,x3+x4=π,则M=x1+x2 +x3+x4=π.(14分)
 (.4分)
(.4分)(2)任取x∈[-π,
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
则f(x)=f(
| π |
| 2 |
又当x≥
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
即f(x)=
|
(3)因为-
| 9 |
| 10 |
| ||
| 2 |
| 9 |
| 10 |
| π |
| 4 |
由对称性得,x1+x2=0,x3+x4=π,则M=x1+x2 +x3+x4=π.(14分)
点评:本题主要考查正弦函数的图象,根的存在性及根的个数判断,以及函数与方程的思想,解答关键是运用数形结合的思想,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
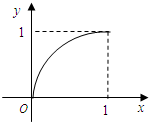 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: