题目内容
 (文做理不做)已知:正四棱锥S-ABCD的高为
(文做理不做)已知:正四棱锥S-ABCD的高为| 3 |
(1)求证:EF∥平面SAD;
(2)试确定点M的位置,使得平面EFM⊥底面ABCD.
分析:(1)取SD中点G,连接AG,FG,易证得AEFG为平行四边形,则AG∥EF,由线面平行的判定定理可得EF∥平面SAD;
(2)连接AC与BD相交点O,取OC中点H,连接SO,FH,EH并延长EH交CD于点M,由平行线分线段成比例定理可得满足条件的M点的位置.
(2)连接AC与BD相交点O,取OC中点H,连接SO,FH,EH并延长EH交CD于点M,由平行线分线段成比例定理可得满足条件的M点的位置.
解答: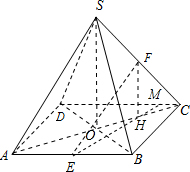 证明:(1)取SD中点G,连接AG,FG,
证明:(1)取SD中点G,连接AG,FG,
则FG∥CD∥AE,FG=
CD∥AE,
∴AEFG为平行四边形,
∴AG∥EF,
∵EF?平面SAD,AG?平面SAD
∴EF∥平面SAD.…(6分)
(2)连接AC与BD相交点O,取OC中点H,连接SO,FH,EH并延长EH交CD于点M,
则SO⊥底面ABCD,FH∥SO,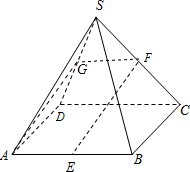
∴FH⊥底面ABCD.
∴平面EFM⊥底面ABCD.
由AB∥CM知,
=
=
,
∴MC=
AE=
AB=
CD
.∴当点M位于CD的
处(距点C)时,平面EFM⊥底面ABCD.…(16分)
 证明:(1)取SD中点G,连接AG,FG,
证明:(1)取SD中点G,连接AG,FG,则FG∥CD∥AE,FG=
| 1 |
| 2 |
∴AEFG为平行四边形,
∴AG∥EF,
∵EF?平面SAD,AG?平面SAD
∴EF∥平面SAD.…(6分)
(2)连接AC与BD相交点O,取OC中点H,连接SO,FH,EH并延长EH交CD于点M,
则SO⊥底面ABCD,FH∥SO,

∴FH⊥底面ABCD.
∴平面EFM⊥底面ABCD.
由AB∥CM知,
| CM |
| AE |
| CH |
| AH |
| 1 |
| 3 |
∴MC=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
.∴当点M位于CD的
| 1 |
| 6 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,熟练掌握空间线面关系的定义及判定是解答的关键.

练习册系列答案
相关题目
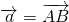 ,
,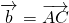 .当实数k为________时k
.当实数k为________时k 与k
与k 互相垂直.
互相垂直.