题目内容
（文做理不做）正方体ABCD-A1B1C1D1中，p、q、r分别是AB、AD、B1C1的中点．那么正方体的过P、Q、R的截面图形是
（理做文不做）已知空间三个点A（-2，0，2）、B（-1，1，2）和C（-3，0，4），设
=
，
=
．当实数k为
+
与k
-2
互相垂直．
正六边形
正六边形
．（理做文不做）已知空间三个点A（-2，0，2）、B（-1，1，2）和C（-3，0，4），设
| a |
| AB |
| b |
| AC |
k=-
或k=2
| 5 |
| 2 |
k=-
或k=2
时k| 5 |
| 2 |
| a |
| b |
| a |
| b |
分析：（文）利用平面的基本性质即可．
（理）利用向量的共线和由数量积判断向量的垂直即可得出．
（理）利用向量的共线和由数量积判断向量的垂直即可得出．
解答：解：（文）如图所示：
正方体的过P、Q、R的截面图形是正六边形PMRSNQ．
下面证明：∵P、Q、R、S分别是AB、AD、B1C1的中点，
∴PQ∥BD∥B1D1∥RS，
∴P、Q、S、R四点共面，
取边BB1的中点M，连接RM并延长交CB的延长线与K点，连接PK．
则△BKM≌△B1RM，∴BK=B1R=BP，
可得Q、P、K三点共线，即M点在平面PQR上，
同理可知N点也在平面PQSR上，
故六点PQNSRM共面．可知其六边长相等．
（理）∵三个点A（-2，0，2）、B（-1，1，2）和C（-3，0，4），
∴
=
=（1，1，0），
=
=（-1，0，2）．
∴k
+
=（k-1，k，2），k
-2
=（k+2，k，-4）．
∵（k
+
）⊥（k
-2
），
∴(k
+
)•(k
-2
)=0，
即（k-1）（k+2）+k2-8=0，化为2k2+k-10=0，解得k=2或k=-
．
故答案为（文）正六边形，（理）k=2或k=-
．
正方体的过P、Q、R的截面图形是正六边形PMRSNQ．
下面证明：∵P、Q、R、S分别是AB、AD、B1C1的中点，
∴PQ∥BD∥B1D1∥RS，
∴P、Q、S、R四点共面，
取边BB1的中点M，连接RM并延长交CB的延长线与K点，连接PK．
则△BKM≌△B1RM，∴BK=B1R=BP，
可得Q、P、K三点共线，即M点在平面PQR上，
同理可知N点也在平面PQSR上，
故六点PQNSRM共面．可知其六边长相等．
（理）∵三个点A（-2，0，2）、B（-1，1，2）和C（-3，0，4），
∴
| a |
| AB |
| b |
| AC |
∴k
| a |
| b |
| a |
| b |
∵（k
| a |
| b |
| a |
| b |
∴(k
| a |
| b |
| a |
| b |
即（k-1）（k+2）+k2-8=0，化为2k2+k-10=0，解得k=2或k=-
| 5 |
| 2 |
故答案为（文）正六边形，（理）k=2或k=-
| 5 |
| 2 |
点评：熟练掌握平面的基本性质和向量的共线与用数量积判断垂直是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
，
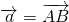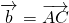．当实数k为________时k
与k
互相垂直．