题目内容
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明![]() )在
)在![]() )上的单调性;
)上的单调性;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为奇函数;(2)证明见解析;(3)
为奇函数;(2)证明见解析;(3)![]() .
.
【解析】试题分析:
本题考查函数奇偶性的判断和单调性的证明,以及根据恒成立问题求参数取值范围。(1)根据奇偶性的判断方法证明。(2)根据单调性的判断方法证明。(3)根据函数的单调性将函数不等式转化为一般不等式,通过分离参数的方法转化为求具体函数的最值问题处理。
试题解析:
(1)![]() 定义域R关于原点对称,
定义域R关于原点对称,
∵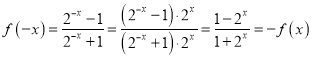 ,
,
![]() 为奇函数.
为奇函数.
(2)证明:设![]() R,且
R,且![]() ,
,
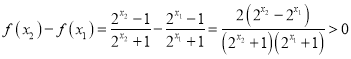 ,
,
∵函数 ![]() 在
在 ![]() 上为增函数,
上为增函数,
![]() ,故
,故![]() ,
,
![]() .
.
∴函数![]() 在
在![]() 上是增函数 .
上是增函数 .
(3)![]()
![]() ,
,
又![]() 为奇函数,
为奇函数,
![]() ,
,
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上为增函数,
上为增函数,
∴当![]() 时,函数
时,函数![]() 取得最小值,且
取得最小值,且![]() 。
。
∴![]() 。
。
故实数![]() 的取值范围为
的取值范围为![]() 。
。

练习册系列答案
相关题目

