题目内容
已知数列{an}（n∈N*）满足：an=logn+1（n+2）（n∈N*）．定义：使a1a2…ak为整数的k值（k∈N*）叫“理想数”，则区间[1，2009]内所有“理想数”的和是________．（注：必要时可利用公式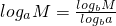
）
2026
分析：根据换底公式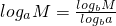：，把an=logn+1（n+2）（n∈N*）代入a1a2…ak并且化简转化为 
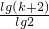为整数m，即k+2=2m，
m∈N*，令m=1，2，3，…，10，可求得区间[1，2009]内的所有“理想数“的和．
解答：根据换底公式：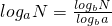
，把an=logn+1（n+2）（n∈N*）代入a1a2…ak有
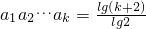=m，m∈N*，
∴k+2=2m，m∈N*．
k分别可取22-2，23-2，24-2…，最大值2m-2≤2009，m最大可取10，
故和为（22-2）+（23-2）+（24-2）+…+（210-2）=2026．
故答案为：2026．
点评：考查数列的综合应用及对数的换底公式，把a1a2…ak化简转化为对数的运算，体现了转化的思想，属中档题．
分析：根据换底公式：
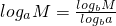，把an=logn+1（n+2）（n∈N*）代入a1a2…ak并且化简转化为 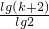为整数m，即k+2=2m，m∈N*，令m=1，2，3，…，10，可求得区间[1，2009]内的所有“理想数“的和．
解答：根据换底公式：
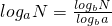，把an=logn+1（n+2）（n∈N*）代入a1a2…ak有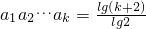=m，m∈N*，∴k+2=2m，m∈N*．
k分别可取22-2，23-2，24-2…，最大值2m-2≤2009，m最大可取10，
故和为（22-2）+（23-2）+（24-2）+…+（210-2）=2026．
故答案为：2026．
点评：考查数列的综合应用及对数的换底公式，把a1a2…ak化简转化为对数的运算，体现了转化的思想，属中档题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目