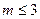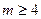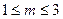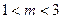题目内容
已知函数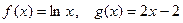 .
.
(1)试判断函数F(x)=(x2+1) f (x) – g(x)在[1,+∞)上的单调性;
(2)当0<a<b时,求证:函数f (x) 定义在区间[a,b]上的值域的长度大于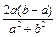 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).
(3)方程f(x)=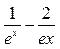 是否存在实数根?说明理由。
是否存在实数根?说明理由。
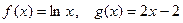 .
.(1)试判断函数F(x)=(x2+1) f (x) – g(x)在[1,+∞)上的单调性;
(2)当0<a<b时,求证:函数f (x) 定义在区间[a,b]上的值域的长度大于
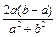 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).(3)方程f(x)=
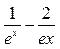 是否存在实数根?说明理由。
是否存在实数根?说明理由。(1)单调递增
(2)略
(3)不存在实数根
(2)略
(3)不存在实数根
(1)∵F(x)=(x2+1)lnx –2 x+2.
x+2.
∴F ′(x)= 2xlnx+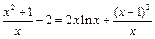 .
.
∴当x≥1时,F ′(x)≥0且仅当x =
′(x)≥0且仅当x = 1时F′(x)=" 0" ∴F(x)在(1,+∞)上单调递增。
1时F′(x)=" 0" ∴F(x)在(1,+∞)上单调递增。
(2)∵0<a<b,f (x)在[a,b]上的值域为[lna,lnb]
∴要证值域的长度大于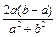 ,
,
即证lnb – lna>
lna>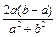
只要证ln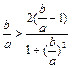
∵0<a<b,∴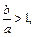 令
令
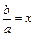
则只要证lnx>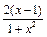 (x>1)
(x>1)
即证(x2+1)l nx –(2x –2)>0 (※)
nx –(2x –2)>0 (※)
由 (1)可知F(x)在(1,+∞)上单调递增∴F(x)>
(1)可知F(x)在(1,+∞)上单调递增∴F(x)> F(1)
F(1) =" 0" 所以(※)式成立.
=" 0" 所以(※)式成立.
∴f (x)在[a, b]上的值域的长度大于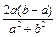 .……9分
.……9分
(3)∵f (x) =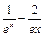
 xlnx=
xlnx=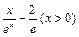
令h (x) = xlnx(x>0).则h ′(x)=lnx+1,
易知,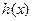 在
在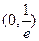 上单调递减,在
上单调递减,在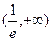 上单调递增
上单调递增
当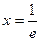 时,
时,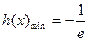
令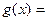
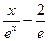 ,则
,则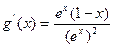
易知, 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
当 时,
时,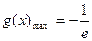
∵ ∴方程f(x)=
∴方程f(x)=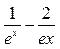 不存在实数根
不存在实数根
 x+2.
x+2.∴F ′(x)= 2xlnx+
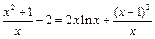 .
.∴当x≥1时,F
 ′(x)≥0且仅当x =
′(x)≥0且仅当x = 1时F′(x)=" 0" ∴F(x)在(1,+∞)上单调递增。
1时F′(x)=" 0" ∴F(x)在(1,+∞)上单调递增。(2)∵0<a<b,f (x)在[a,b]上的值域为[lna,lnb]
∴要证值域的长度大于
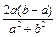 ,
,即证lnb –
 lna>
lna>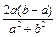
只要证ln
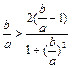
∵0<a<b,∴
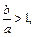 令
令
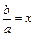
则只要证lnx>
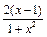 (x>1)
(x>1)即证(x2+1)l
 nx –(2x –2)>0 (※)
nx –(2x –2)>0 (※)由
 (1)可知F(x)在(1,+∞)上单调递增∴F(x)>
(1)可知F(x)在(1,+∞)上单调递增∴F(x)> F(1)
F(1) =" 0" 所以(※)式成立.
=" 0" 所以(※)式成立.∴f (x)在[a, b]上的值域的长度大于
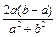 .……9分
.……9分(3)∵f (x) =
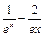
 xlnx=
xlnx=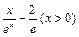
令h (x) = xlnx(x>0).则h ′(x)=lnx+1,
易知,
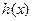 在
在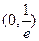 上单调递减,在
上单调递减,在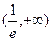 上单调递增
上单调递增当
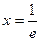 时,
时,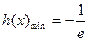
令
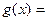
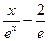 ,则
,则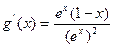
易知,
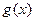 在
在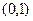 上单调递增,在
上单调递增,在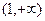 上单调递减
上单调递减当
 时,
时,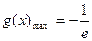
∵
 ∴方程f(x)=
∴方程f(x)=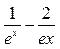 不存在实数根
不存在实数根
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的定义域是____________________.
的定义域是____________________.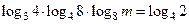 ,求
,求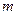 的值.
的值. 的图象是
的图象是



 的图象经过点A,若点A在直线
的图象经过点A,若点A在直线 上,其中
上,其中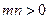 ,则
,则 的最小值为
的最小值为 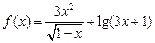 的定义域是___________.
的定义域是___________. ,且
,且 ,则
,则 的取值范围是
的取值范围是



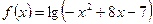 在(m,m+1)上是增函数,则m取值范围是( )
在(m,m+1)上是增函数,则m取值范围是( )