题目内容
设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D.
(Ⅰ)求点D的坐标;
(Ⅱ)当△ABC的面积大于1时, 求实数a的取值范围.
(Ⅰ)求点D的坐标;
(Ⅱ)当△ABC的面积大于1时, 求实数a的取值范围.
0< a<2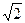 -2.
-2.
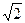 -2.
-2.(Ⅰ)易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4)),
所以由中点公式得D(a+2, log2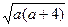 ).
).
(Ⅱ)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2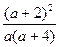 ,
,
其中A′,B′,C′为A,B,C在x轴上的射影.
由S△ABC= log2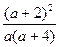 >1, 得0< a<2
>1, 得0< a<2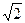 -2.
-2.
所以由中点公式得D(a+2, log2
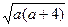 ).
). (Ⅱ)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2
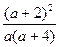 ,
, 其中A′,B′,C′为A,B,C在x轴上的射影.
由S△ABC= log2
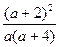 >1, 得0< a<2
>1, 得0< a<2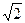 -2.
-2.
练习册系列答案
相关题目
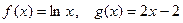 .
.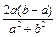 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).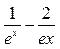 是否存在实数根?说明理由。
是否存在实数根?说明理由。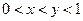 ,则( )
,则( )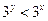
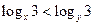

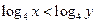
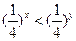
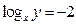 ,则
,则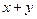 的最小值是( )
的最小值是( )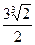
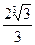
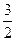
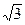
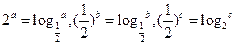 ,则( )
,则( )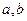 表示
表示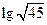 的值为 .
的值为 .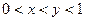 ,则 ( )
,则 ( )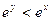
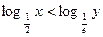
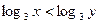
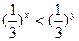
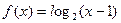 的定义域为 .
的定义域为 .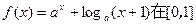 上的最大值和最小值之和为a,若f(x)的零点在(m,m+1)内,则a= ,整数m= 。
上的最大值和最小值之和为a,若f(x)的零点在(m,m+1)内,则a= ,整数m= 。