题目内容
（2013•太原一模）x、y满足约束条件
，若目标函数z=ax+by（a＞0，b＞0）的最大值为7，则
+
的最小值为（ ）
|
| 3 |
| a |
| 4 |
| b |
分析：作出可行域，得到目标函数z=ax+by（a＞0，b＞0）的最优解，从而得到3a+4b=7，利用基本不等式即可．
解答：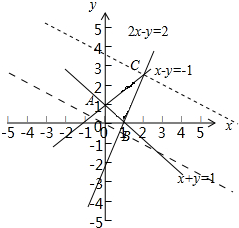
解：∵x、y满足约束条件
，目标函数z=ax+by（a＞0，b＞0），作出可行域：
由图可得，可行域为△ABC区域，目标函数z=ax+by（a＞0，b＞0）经过可行域内的点C时，取得最大值（最优解）．
由
解得x=3，y=4，即C（3，4），
∵目标函数z=ax+by（a＞0，b＞0）的最大值为7，
∴3a+4b=7（a＞0，b＞0），
∴
+
=
（3a+4b）•（
+
）
=
（9+
+16+
）≥
（25+2
）=
×49=7（当且仅当a=b=1时取“=”）．
故选B．
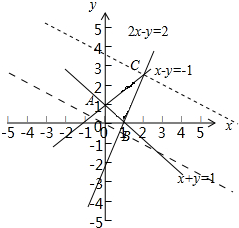解：∵x、y满足约束条件
|
由图可得，可行域为△ABC区域，目标函数z=ax+by（a＞0，b＞0）经过可行域内的点C时，取得最大值（最优解）．
由
|
∵目标函数z=ax+by（a＞0，b＞0）的最大值为7，
∴3a+4b=7（a＞0，b＞0），
∴
| 3 |
| a |
| 4 |
| b |
| 1 |
| 7 |
| 3 |
| a |
| 4 |
| b |
=
| 1 |
| 7 |
| 12b |
| a |
| 12a |
| b |
| 1 |
| 7 |
|
| 1 |
| 7 |
故选B．
点评：本题考查线性规划，作出线性约束条件下的可行域，求得其最优解是关键，也是难点，属于中档题．
练习册系列答案
相关题目