题目内容
以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
| A.(x-1)2+(y+2)2=100 |
| B.(x-1)2+(y-2)2=100 |
| C.(x-1)2+(y-2)2=25 |
| D.(x+1)2+(y+2)2=25 |
C
分析:要求圆的方程,即要求圆心坐标和半径,由AB为所求圆的直径,利用中点坐标公式求出线段AB的中点坐标即为圆心坐标,再利用两点间的距离公式求出线段AC的长度即为圆的半径,根据圆心坐标和半径写出圆的标准方程即可.
解:设线段AB的中点为C,则C的坐标为(
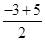 ,
,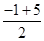 )即为(1,2),
)即为(1,2),所求圆的圆心坐标为(1,2);
又|AC|=
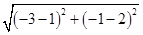 =5,则圆的半径为5,
=5,则圆的半径为5,所以所求圆的标准方程为:(x-1)2+(y-2)2=25.
故选C

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
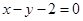 被圆
被圆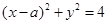 截得的弦长为
截得的弦长为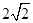 ,则实数
,则实数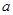 的值为
的值为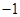 或
或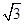
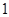 或
或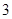
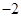 或
或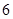
 平分∠ABC
平分∠ABC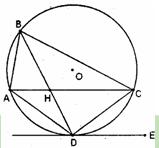
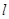 与圆C
与圆C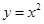
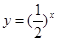
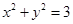
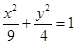

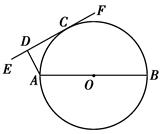
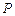 ,则点
,则点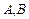 距离之和的最大值为 ▲ .
距离之和的最大值为 ▲ .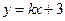 与圆
与圆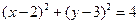 相交于
相交于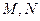 两 点,若
两 点,若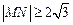 ,则
,则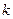 的取值范围是
的取值范围是 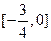
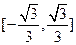
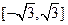
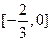
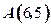 、
、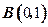 两点,并且圆心在直线
两点,并且圆心在直线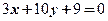 的圆的方程是 。
的圆的方程是 。