题目内容
【题目】从某居民区随机抽取![]() 个家庭,获得第
个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为![]() 千元,预测该家庭的月储蓄.其中
千元,预测该家庭的月储蓄.其中![]() ,
,![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为![]() ,附:线性回归方程
,附:线性回归方程![]() 中,
中, 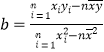 ,
,![]() .
.
【答案】(1)![]() ;(2)见解析;(3)1.7(千元)
;(2)见解析;(3)1.7(千元)
【解析】
(1)由题意求出![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,代入公式求值
,代入公式求值![]() ,又由
,又由![]() =
=![]() ﹣
﹣![]() ,得出
,得出![]() 从而得到回归直线方程;
从而得到回归直线方程;
(2)变量y的值随x的值增加而增加,可知x与y之间是正相关还是负相关.
(3)代入x=7即可预测该家庭的月储蓄.
(1)由题意知,n=10,![]() xi=80,
xi=80,![]() yi=20,
yi=20,
∴![]() =
=![]() ,
,![]() =
=![]()
那么:n![]()
![]() =10×8×2=160,n
=10×8×2=160,n![]() 2=10×64=640.
2=10×64=640.
![]() xiyi=184,
xiyi=184,![]() x
x![]() =720.
=720.
由![]() =
=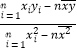 =
=![]() .
.
![]() =
=![]() ﹣
﹣![]() =2﹣0.3×8=﹣0.4,
=2﹣0.3×8=﹣0.4,
故所求回归方程为y=0.3x﹣0.4.
(2)由于变量y的值随x的值增加而增加,即![]() =0.3>0.
=0.3>0.
故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为y=0.3×7﹣0.4=1.7(千元).

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
【题目】探究函数![]() ,x∈(0,+∞)取最小值时x的值,列表如下:
,x∈(0,+∞)取最小值时x的值,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题:
(1)函数![]() (x>0)在区间(0,2)上递减;函数
(x>0)在区间(0,2)上递减;函数![]() 在区间________上递增.当x=_________时,
在区间________上递增.当x=_________时,![]() _______.
_______.
(2)证明:函数![]() (x>0)在区间(O,2)上递减.
(x>0)在区间(O,2)上递减.