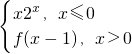题目内容
设函数f(x)满足f(0)=1,且对任意x,y∈R,都有f(xy+1)=f(x)f(y)-f(y)-x+2.(Ⅰ)求f(x)的解析式;
(Ⅱ)若数列{an}满足:an+1=3f(an)-1(n∈N+),且a1=1,求数列{an}的通项;
(Ⅲ)求证:
| 3 |
| 2 |
| 1 |
| 2f(n-1) |
分析:(Ⅰ)运用赋值的方法,令x=y=0,求出f(1)=2,再令y=0可得f(x)的解析式;
(Ⅱ)运用待定系数法,找出an+1+1与an+1的位数关系,结合等比数列的通项公式,求出数列{an}的通项;
(Ⅲ)运用二项式定理,结合不等式的知识与放缩法,从而证出不等式恒成立.
(Ⅱ)运用待定系数法,找出an+1+1与an+1的位数关系,结合等比数列的通项公式,求出数列{an}的通项;
(Ⅲ)运用二项式定理,结合不等式的知识与放缩法,从而证出不等式恒成立.
解答:解:(Ⅰ)因f(0)=1.
若令x=y=0,得f(1)=f(0)f(0)-f(0)-0+2=2
再令y=0得f(1)=f(x)f(0)-f(0)-x+2,可得f(x)=x+1,x∈R
(Ⅱ)∵f(x)=x+1,∴an+1=3f(an)-1=3(an+1)-1=3an+2,
∴an+1+1=3(an+1),又a1+1=2,∴数列{an+1}是首项为2,公比为3的等比数列,
∴an+1=2•3n-1,即an=2•3n-1-1
(Ⅲ)∵f(x)=x+1,x∈R,∴T=[1+
]f(n-1)=(1+
)n,n∈N*
T=
+
(
)+
(
)2+
(
)3+…+
(
)r+≥1+n•
=
另一方面:因为
(
)r=
•(
)r≤(
)r,
所以T≤1+
+(
)2+…+(
)r+…+(
)n
=
=2(1-
)=2-
<2.
综上可得命题成立.
若令x=y=0,得f(1)=f(0)f(0)-f(0)-0+2=2
再令y=0得f(1)=f(x)f(0)-f(0)-x+2,可得f(x)=x+1,x∈R
(Ⅱ)∵f(x)=x+1,∴an+1=3f(an)-1=3(an+1)-1=3an+2,
∴an+1+1=3(an+1),又a1+1=2,∴数列{an+1}是首项为2,公比为3的等比数列,
∴an+1=2•3n-1,即an=2•3n-1-1
(Ⅲ)∵f(x)=x+1,x∈R,∴T=[1+
| 1 |
| 2f(n-1) |
| 1 |
| 2n |
T=
| C | 0 n |
| C | 1 n |
| 1 |
| 2n |
| C | 2 n |
| 1 |
| 2n |
| C | 3 n |
| 1 |
| 2n |
| C | r n |
| 1 |
| 2n |
| 1 |
| 2n |
| 3 |
| 2 |
另一方面:因为
| C | r n |
| 1 |
| 2n |
| m(n-1)(n-2)-(n-r+1) |
| nr•1•2•3…r |
| 1 |
| 2 |
| 1 |
| 2 |
所以T≤1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
1-(
| ||
1-
|
| 1 |
| 2n+1 |
| 1 |
| 2n |
综上可得命题成立.
点评:数列与不等式相综合是考试的热点,也是难点.第一小问赋值的同进应该注意一个“巧”字,不要出现重复累赘,不得其法;第二小问除待定系数的方法外还可利用利用作差构造新数列的方法,同学们不妨作个尝试;第三小问证明不等式恒成立,在结合二项式定理的同时还要注意式子的适当放缩,从而达到证明的目的.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知定义在R上的函数f(x)满足:对任意x∈R,都有f(x)=f(2-x)成立,且当x∈(-∞,1)时,(x-1)f′(x)<0(其中f'(x)为f(x)的导数).设a=f(0),b=f(
),c=f(3),则a、b、c三者的大小关系是( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |
设函数f(x)满足f(n+1)=
(n∈N*),且f(1)=2,则f(20)为( )
| 2f(n)+n |
| 2 |
| A、95 | B、97 |
| C、105 | D、192 |