若a＞b＞0.则( )A．ab＜b2B．a＞bC．log${\;} {\frac{1}{2}}$a＞log${\;} {\frac{1}{2}}$bD．a2＞b2 题目和参考答案——青夏教育精英家教网——

题目内容

18．若a＞b＞0，则（　　）

	A．	ab＜b²		B．	（$\frac{1}{2}$）^a＞（$\frac{1}{2}$）^b
	C．	log${\;}_{\frac{1}{2}}$a＞log${\;}_{\frac{1}{2}}$b		D．	a²＞b²

分析利用指数函数与对数函数的单调性即可得出．

解答解：∵a＞b＞0，
∴ab＞b²，$（\frac{1}{2}）^{a}＜（\frac{1}{2}）^{b}$，$lo{g}_{\frac{1}{2}}a＜$$lo{g}_{\frac{1}{2}}b$，a²＞b²．
因此A．B．C．不正确，D正确．
故选：D．

点评本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

8．设集合M={x|-3≤x＜7}，N={x|2x+k≤0}，M∩N≠∅，则k的取值范围为k≤6．

9．已知函数f（x）=$\frac{x}{1+{x}^{2}}$是定义在（-1，1）上的函数，
（1）试判断f（x）的奇偶性；
（2）用定义证明f（x）在（-1，1）上是增函数；
（3）解不等式f（x-1）+f（x）＜0．

6．函数f（x）是R上的奇函数，且当x＞0时，函数的解析式为f（x）=$\frac{2}{x}$-1．
（1）用定义证明f（x）在（0，+∞）上是减函数；
（2）求当x＜0时，函数的解析式．
（3）用分段函数形式写出函数f（x）在R上的解析式．当f（a）=3时，求a的值．

13．已知函数f（x）=x²-2x+1+alnx有两个极值点x₁，x₂，且x₁＜x₂，则实数a的取值范围为（　　）

$（{-∞，\frac{1}{2}}）$

$（{0，\frac{1}{2}}）$

$（{\frac{1}{2}，+∞}）$

$（{0，\frac{1}{2}}]$

3．已知$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（1，1），且（$\overrightarrow{a}$+$λ\overrightarrow{b}$）$⊥\overrightarrow{a}$，则λ=-1．

10．函数f（x）=sinx-2cosx=$\sqrt{5}$sin（x+φ），则cosφ等于（　　）

$\frac{\sqrt{5}}{5}$

$\frac{2\sqrt{5}}{5}$

-$\frac{2\sqrt{5}}{5}$

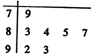七位评委为某跳水运动员打出的分数的茎叶图如图，其极差为14．

8．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$=（-1，1），$\overrightarrow{b}$=（2，3），$\overrightarrow{c}$=（-2，k），若（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k的值为$\frac{1}{2}$．