题目内容
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 的取值仅能是2;(3)详见解析.
的取值仅能是2;(3)详见解析.
【解析】
试题(1)由数组的极差的定义,可知,![]() ,这时三数为
,这时三数为![]() ,第二次操作后,
,第二次操作后,![]() ,这时三数为
,这时三数为![]() ,第三次操作后,
,第三次操作后,![]() ,,这时三数为
,,这时三数为![]() ,第四次操作后,
,第四次操作后,![]() ,这时三数为
,这时三数为![]() ,第五次操作后,
,第五次操作后,![]() ,这时三数为
,这时三数为![]() ,第六次操作后,
,第六次操作后,![]() ,这时三数为
,这时三数为![]() ,
,![]() ,第2014次操作后,
,第2014次操作后,![]() ,这时三数为
,这时三数为![]() ;(2)已知
;(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,这时极差
,这时极差![]() 最小值为
最小值为![]() ,当
,当![]() 时,这时
时,这时![]() 是三个连续的正整数,即为
是三个连续的正整数,即为![]() ,由(1)可知,通过变化后,所得数仍然是
,由(1)可知,通过变化后,所得数仍然是![]() ,所以数组的极差不会改变,即
,所以数组的极差不会改变,即![]() ,符合题意,当
,符合题意,当![]() ,这时
,这时![]() 三个数,通过变化成
三个数,通过变化成![]() ,这是极差为
,这是极差为![]() ,或
,或![]() ,这样就可以确定出
,这样就可以确定出![]() 的取值仅能是2;(3)若
的取值仅能是2;(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() ,这时
,这时![]() 三数形式为
三数形式为![]() ,由二项式定理可知
,由二项式定理可知![]() ,故所以
,故所以![]() 的极差
的极差![]() 是3的倍数,这样根据极差的定义,通过操作,得到
是3的倍数,这样根据极差的定义,通过操作,得到![]() 是一个公差为
是一个公差为![]() 的等差数列,从而可得出结论.
的等差数列,从而可得出结论.
(1)![]() ,
,![]() ,
,![]() 3分
3分
(2)法一:
①当![]() 时,则
时,则![]()
所以![]() ,
,![]() ,
,
由操作规则可知,每次操作,数组中的最大数![]() 变为最小数
变为最小数![]() ,最小数
,最小数![]() 和次
和次
小数![]() 分别变为次小数
分别变为次小数![]() 和最大数
和最大数![]() ,所以数组的极差不会改变.
,所以数组的极差不会改变.
所以,当![]() 时,
时,![]() 恒成立.
恒成立.
②当![]() 时,则
时,则![]()
所以![]() 或
或![]()
所以总有![]() .
.
综上讨论,满足![]() 的
的![]() 的取值仅能是2. 8分
的取值仅能是2. 8分
法二:
因为![]() ,所以数组
,所以数组![]() 的极差
的极差![]()
所以![]() ,
,
若![]() 为最大数,则
为最大数,则![]()
若![]() ,则
,则![]()
若![]() ,则
,则![]() ,
,
当![]() 时,可得
时,可得![]() ,即
,即![]()
由![]() 可得
可得![]()
所以![]()
将![]() 代入
代入![]() 得
得![]()
所以当![]() 时,
时,![]() (
(![]() )
)
由操作规则可知,每次操作,数组中的最大数![]() 变为最小数
变为最小数![]() ,最小数
,最小数![]() 和次小
和次小
数![]() 分别变为次小数
分别变为次小数![]() 和最大数
和最大数![]() ,所以数组的极差不会改变.
,所以数组的极差不会改变.
所以满足![]() 的
的![]() 的取值仅能是2. 8分
的取值仅能是2. 8分
(3)因为![]() 是以4为公比的正整数等比数列的三项,
是以4为公比的正整数等比数列的三项,
所以![]() 是形如
是形如![]() (其中
(其中![]() )的数,
)的数,
又因为![]()
所以![]() 中每两个数的差都是3的倍数.
中每两个数的差都是3的倍数.
所以![]() 的极差
的极差![]() 是3的倍数. 9分
是3的倍数. 9分
法1:设![]() ,不妨设
,不妨设![]() ,
,
依据操作![]() 的规则,当在三元数组
的规则,当在三元数组![]() (
(![]() ,
,![]() )中,总满足
)中,总满足![]() 是唯一最大数,
是唯一最大数,![]() 是最小数时,一定有
是最小数时,一定有![]() ,解得
,解得![]() .
.
所以,当![]() 时,
时,![]() .
.
![]() ,
,![]()
依据操作![]() 的规则,当在三元数组
的规则,当在三元数组![]() (
(![]() ,
,![]() )中,总满足
)中,总满足![]() 是最大数,
是最大数,![]() 是最小数时,一定有
是最小数时,一定有![]() ,解得
,解得![]() .
.
所以,当![]() 时,
时,![]() .
.
![]() ,
,![]()
所以存在![]() ,满足
,满足![]() 的极差
的极差![]() . 13分
. 13分
法2:设![]() ,则
,则
①当![]() 中有唯一最大数时,不妨设
中有唯一最大数时,不妨设![]() ,则
,则
![]() ,
,
所以![]()
所以,若![]() 是3的倍数,则
是3的倍数,则![]() 是3的倍数.
是3的倍数.
所以![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
所以![]() 11分
11分
②当![]() 中的最大数有两个时,不妨设
中的最大数有两个时,不妨设![]() ,则
,则
![]() ,
,
所以![]() ,
,
所以,若![]() 是3的倍数,则
是3的倍数,则![]() 是3的倍数.
是3的倍数.
所以![]() ,则
,则![]() ,
,![]()
所以![]() .
.
所以当![]() 时,数列
时,数列![]() 是公差为3的等差数列. 12分
是公差为3的等差数列. 12分
当![]() 时,由上述分析可得
时,由上述分析可得![]() ,此时
,此时![]()
所以存在![]() ,满足
,满足![]() 的极差
的极差![]() . 13分
. 13分

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
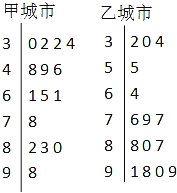
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)