题目内容
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F、M分别是A1C1、A1D和B1A上任一点,求证:平面A1EF∥平面B1MC.
见解析
如图建立空间直角坐标系,
则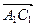 =(-1,1,0),
=(-1,1,0), =(-1,0,-1)
=(-1,0,-1)
 =(1,0,1),
=(1,0,1), 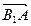 =(0,-1,-1)
=(0,-1,-1)
设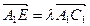 ,
, ,
,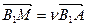 (
(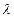 、
、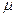 、
、
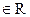 ,且均不为0)
,且均不为0)
设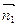 、
、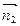 分别是平面A1EF与平面B1MC的法向量,
分别是平面A1EF与平面B1MC的法向量,


 由
由  可得
可得 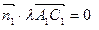 即
即 
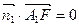


解得: =(1,1,-1)
=(1,1,-1)


 由
由 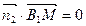 可得
可得 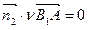 即
即 
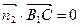
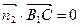
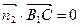
解得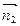 =(-1,1,-1),所以
=(-1,1,-1),所以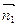 =-
=-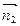 ,
, 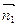 ∥
∥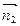 ,
,
所以平面A1EF∥平面B1MC.
注:如果求证的是两个平面垂直,也可以求出两个平面的法向量后,利用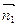 ⊥
⊥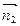
 来证明.
来证明.
则
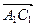 =(-1,1,0),
=(-1,1,0), =(-1,0,-1)
=(-1,0,-1) =(1,0,1),
=(1,0,1), 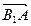 =(0,-1,-1)
=(0,-1,-1)设
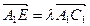 ,
, ,
,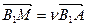 (
(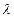 、
、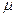 、
、
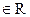 ,且均不为0)
,且均不为0)设
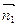 、
、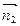 分别是平面A1EF与平面B1MC的法向量,
分别是平面A1EF与平面B1MC的法向量,

 由
由  可得
可得 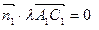 即
即 
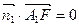


解得:
 =(1,1,-1)
=(1,1,-1)

 由
由 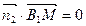 可得
可得 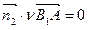 即
即 
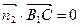
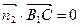
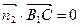
解得
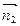 =(-1,1,-1),所以
=(-1,1,-1),所以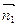 =-
=-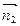 ,
, 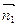 ∥
∥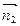 ,
,所以平面A1EF∥平面B1MC.
注:如果求证的是两个平面垂直,也可以求出两个平面的法向量后,利用
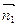 ⊥
⊥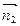
 来证明.
来证明.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
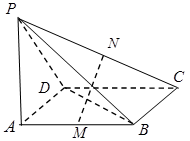
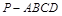 的底面
的底面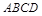 是正方形,侧棱
是正方形,侧棱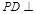 底面
底面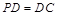 ,
,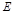 是
是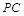 的中点.
的中点.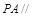 平面
平面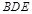 ;
;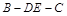 的余弦值.
的余弦值.
 中,
中, 为
为 的中点,则异面直线
的中点,则异面直线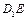 和
和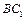 间的距离 .
间的距离 .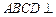 平面
平面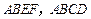 是正方形,
是正方形,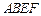 是矩形,且
是矩形,且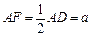 ,
,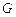 是
是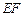 的中点.
的中点.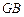 与平面
与平面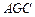 所成角
所成角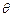 的正弦值;
的正弦值;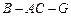 的余弦值.
的余弦值.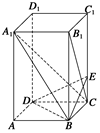 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.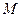 是PC的中点,设
是PC的中点,设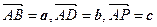 .
.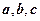 表示出向量
表示出向量 ;
;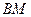 的长.
的长.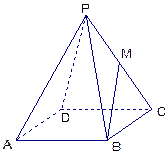
 分别是
分别是 轴,
轴,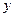 轴正方向上的单位向量,
轴正方向上的单位向量,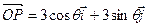 ,
,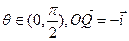 。若用?来表示
。若用?来表示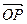 与
与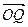 的夹角,则?等于 ( )
的夹角,则?等于 ( )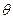
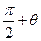
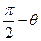
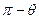
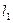 的方向向量为
的方向向量为 ,直线
,直线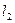 的方向向量为
的方向向量为 ,那么
,那么