题目内容
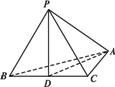
设P是△ABC所在平面外一点，P到A、B、C的距离相等，∠BAC为直角．
求证：平面PCB⊥平面ABC．
答案：
解析：
解析：
|
证明：如图所示，取BC的中点D，连结PD、AD，∵D是Rt△ABC的斜边BC的中点，∴BD＝CD＝AD．又PA＝PB＝PC，PD是公共边，∴∠PDA＝∠PDB＝∠PDC＝90°． ∴PD⊥BC，PD⊥DA，PD⊥平面ABC． 又PD
|
平面PCB，∴平面PCB⊥平面ABC．
练习册系列答案
名校课堂系列答案
相关题目
设P是△ABC所在平面α外一点，H是P在α内的射影，且PA，PB，PC与α所成的角相等，则H是△ABC的（ ）
| A、内心 | B、外心 | C、垂心 | D、重心 |