题目内容
24、设P是△ABC所在平面外一点，P和A、B、C的距离相等，∠BAC为直角．
求证：平面PCB⊥平面ABC．
求证：平面PCB⊥平面ABC．
分析：欲证平面PCB⊥平面ABC，根据面面垂直的判定定理可知在平面PCB内一直线与平面ABC垂直，取BC的中点D，连接PD、AD，
根据线面垂直的判定定理可知PD⊥平面ABC，而PD?平面PCB，满足定理所需条件．
根据线面垂直的判定定理可知PD⊥平面ABC，而PD?平面PCB，满足定理所需条件．
解答：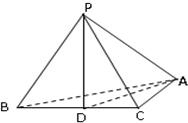
证明：如答图所示，取BC的中点D，连接PD、AD，
∵D是直角三角形ABC的斜边BC的中点
∴BD=CD=AD，又PA=PB=PC，PD是公共边
∴∠PDA=∠PDB=∠POC=90°
∴PD⊥BC，PD⊥DA，PD⊥平面ABC
∴又PD?平面PCB
∴平面PCB⊥平面ABC．
证明：如答图所示，取BC的中点D，连接PD、AD，∵D是直角三角形ABC的斜边BC的中点
∴BD=CD=AD，又PA=PB=PC，PD是公共边
∴∠PDA=∠PDB=∠POC=90°
∴PD⊥BC，PD⊥DA，PD⊥平面ABC
∴又PD?平面PCB
∴平面PCB⊥平面ABC．
点评：本题主要考查了平面与平面垂直的判定，应熟练记忆平面与平面垂直的判定定理，属于基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设P是△ABC所在平面α外一点，H是P在α内的射影，且PA，PB，PC与α所成的角相等，则H是△ABC的（ ）
| A、内心 | B、外心 | C、垂心 | D、重心 |