题目内容

用数学归纳法证明命题“n3+(n+1)3+(n+2)3(n∈N)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开(　　　)

A.(k+3)3　　　　　　　　　B.(k+2)3

C.(k+1)3　　　　　　　　 　　D.(k+1)3+(k+2)3

分析　本题考查用数学归纳法证明整除性问题.只需把n=k+1时的情况拼凑成一部分为假设的形式,另一部分为除数的倍数形式即可.

解　当n=k+1时,被除数为(k+1)3+(k+2)3+(k+3)3=k3+(k+1)3+(k+2)3+9(k2+3k+3).故只需展开(k+3)3即可.

答案　A

练习册系列答案
相关题目
16、用数学归纳法证明命题：
（n+1）×（n+2）×…×（n+n）=2n×1×3×…×（2n-1）
有下列说法
①若数列〔an〕的前n项和是Sn=an2+bn+c，其中abc是常数，则数列〔an〕一定不是等差数列：
②若
AB
=3
a
，
CD
=-2
a
，且|
AD
|=|
BC
|，则四边形ABCD是等腰梯形；
③“x=-1”是“x2-5x-6=0”的必要不充分条件；
④用数学归纳法证明命题：
1
2
+
1
4
+
1
8
+…+
1
2n
＜1，在第二步由n=k到n=k+1时，不等式左边增加了l项．
其中正确说法的序号是
 
．
用数学归纳法证明命题时，某命题左式为
1
2
+
1
3
+
1
4
+…+
1
2n-1
，则n=k+1与n=k时相比，左边应添加的项为（　　）
用数学归纳法证明命题“当n为正奇数时，xn+yn能被x+y整除”时，在验证n=1正确后，归纳假设应写成（    ）

A.假设n=k（k∈N*）时，xk+yk能被x+y整除

B.假设n≤k（k≥1）时，xk+yk能被x+y整除

C.假设n=2k+1（k∈N*）时，x2k+1+y2k+1能被x+y整除

D.假设n=2k-1（k∈N*）时，x2k-1+y2k-1能被x+y整除

用数学归纳法证明命题：，从“第步到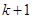步”时，两边应同时加上        ．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网