题目内容
用数学归纳法证明命题时,某命题左式为
+
+
+…+
,则n=k+1与n=k时相比,左边应添加的项为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
分析:n=k时,最后一项为
,n=k+1时,最后一项为
,由此可得由n=k变到n=k+1时,左边增加的项即可.
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
解答:解:由题意,n=k时,最后一项为
,n=k+1时,最后一项为
,
∴由n=k变到n=k+1时,左边增加了
+
+
+L+
,
故选B.
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
∴由n=k变到n=k+1时,左边增加了
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| 2k+1-1 |
故选B.
点评:本题考查数学归纳法,考查学生分析解决问题的能力,找出规律是解题的关键,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 ,从“第
,从“第 步到
步到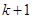 步”时,两边应同时加上 .
步”时,两边应同时加上 .