题目内容
用数学归纳法证明命题“当n为正奇数时,xn+yn能被x+y整除”时,在验证n=1正确后,归纳假设应写成( )A.假设n=k(k∈N*)时,xk+yk能被x+y整除
B.假设n≤k(k≥1)时,xk+yk能被x+y整除
C.假设n=2k+1(k∈N*)时,x2k+1+y2k+1能被x+y整除
D.假设n=2k-1(k∈N*)时,x2k-1+y2k-1能被x+y整除
解析:A、B中的k不一定为正奇数,C中,k=1时,n=3,不是从n=1开始,故选D.
答案:D

练习册系列答案
相关题目
 ,从“第
,从“第 步到
步到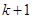 步”时,两边应同时加上 .
步”时,两边应同时加上 .