题目内容
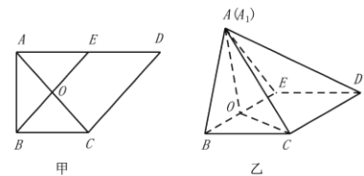
【题目】如图,椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,
, ![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .
.
(1)若点![]() 坐标为
坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)延长![]() 交椭圆
交椭圆![]() 与点
与点![]() ,若直线
,若直线![]() 的斜率是直线
的斜率是直线![]() 的斜率的3倍,求椭圆
的斜率的3倍,求椭圆![]() 的离心率;
的离心率;
(3)是否存在椭圆![]() ,使直线
,使直线![]() 平分线段
平分线段![]() ?
?
【答案】(1)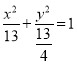 ;(2)
;(2)![]() ;(3)存在.
;(3)存在.
【解析】试题分析:(1)由椭圆的标准方程,可得![]() ,进而得到
,进而得到![]() ,再把点
,再把点![]() 代入椭圆的方程,即可求解椭圆的标准方程;
代入椭圆的方程,即可求解椭圆的标准方程;
(2)由直线![]() 的方程与椭圆的方程联立,利用根据与系数的关系,得到
的方程与椭圆的方程联立,利用根据与系数的关系,得到![]() 的坐标,再由
的坐标,再由![]() ,化简即可求解椭圆的离心率.
,化简即可求解椭圆的离心率.
(3)设![]() 与
与![]() 交于
交于![]() 点,用直线
点,用直线![]() 的方程与
的方程与![]() 联立,求解
联立,求解![]() 点坐标,再把点
点坐标,再把点![]() 的坐标代入椭圆的方程,令
的坐标代入椭圆的方程,令![]() ,转化为函数
,转化为函数![]() 恒成立,利用二次函数的性质,即可求解结论.
恒成立,利用二次函数的性质,即可求解结论.
试题解析:(1)![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() .又
.又![]() ,
, ![]() .
.
![]() ,
, ![]() .
.![]() 方程为
方程为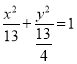 .
.

(2)![]() :
: ![]() 与
与![]() 联立,得,
联立,得,
![]() .
.![]() ,
, ![]() .
.
又![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
(3)![]() :
: ![]() .设
.设![]() 与
与![]() 交于
交于![]() 点,
点,
由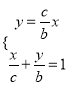 ,得
,得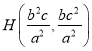 .
.
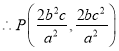 代入椭圆方程,得,
代入椭圆方程,得,
![]() ,令
,令![]() ,
,
得![]() ,设
,设![]() ,
,
![]() 恒成立,
恒成立, ![]() 在
在![]() 上递增.
上递增.
又![]() ,
, ![]() ,
,
![]() 在
在![]() 存在
存在![]() ,使
,使![]() ,
,
![]() 存在椭圆
存在椭圆![]() ,使
,使![]() 平分线段
平分线段![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目