题目内容
设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( ).
| A.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件 |
| B.当m?α时,“m⊥β”是“α⊥β”的充分不必要条件 |
| C.当m?α时,“n∥α”是“m∥n”必要不充分条件 |
| D.当m?α时,“n⊥α”是“m⊥n”的充分不必要条件 |
C
解析

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=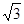 ,则异面直线AD,BC所成的角为( )
,则异面直线AD,BC所成的角为( )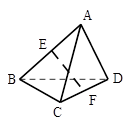
| A.30° | B.60° | C.90° | D.120° |
 -
- 为正方体,下列结论错误的是( )
为正方体,下列结论错误的是( )
A. ∥ ∥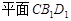 | B.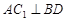 |
C.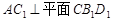 | D.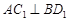 |
正方体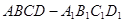 中,点
中,点 是
是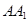 的中点,
的中点,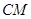 和
和 所成角的余弦值为( )
所成角的余弦值为( )
A.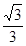 | B.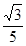 | C.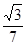 | D. |
设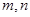 为两条直线,
为两条直线, 为两个平面,下列四个命题中正确的是
为两个平面,下列四个命题中正确的是
A.若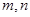 与 与 所成的角相等,则 所成的角相等,则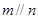 |
B.若 , ,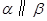 ,则 ,则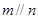 |
C.若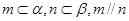 ,则 ,则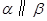 |
D.若 ,则 ,则 |
已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( )
| A.与a,b都相交 |
| B.只能与a,b中的一条相交 |
| C.至少与a,b中的一条相交 |
| D.与a,b都平行 |
下面四个命题:
①“直线a∥直线b”的充分条件是“直线a平行于直线b所在的平面”;
②“直线l⊥平面α”的充要条件是“直线垂直平面α内无数条直线”;
③“直线a,b不相交”的必要不充分条件是“直线a,b为异面直线”;
④“平面α∥平面β”的必要不充分条件是“平面α内存在不共线三点到平面β的距离相等”.
其中为真命题的序号是( )
| A.①② | B.②③ | C.③④ | D.④ |
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 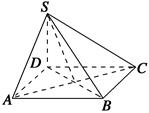
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |