题目内容
如果随机变量ξ～N（0，σ2），且P（-2＜ξ≤0）=0.4，则P（ξ＞2）等于（ ）
分析：本题考查正态分布曲线的性质，随机变量ξ服从正态分布N（0，σ2），由此知曲线的对称轴为Y轴，P（-2≤ξ≤2）=2P（-2＜ξ≤0），又P（ξ＞2）=
[1-P（-2≤ξ≤2）]，再由P（-2＜ξ≤0）=0.4，可得答案．
| 1 |
| 2 |
解答：解：∵随机变量ξ服从正态分布N（0，σ2），且P（-2≤ξ≤0）=0.4，
∴P（-2≤ξ≤2）=0.8
∴P（ξ＞2）=
[1-P（-2≤ξ≤2）]=
[1-0.8]=0.1．
故选A．
∴P（-2≤ξ≤2）=0.8
∴P（ξ＞2）=
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查正态分布曲线的重点及曲线所表示的意义，解题的关键是正确正态分布曲线的重点及曲线所表示的意义，由曲线的对称性求出概率，本题是一个数形结合的题．
练习册系列答案
小题狂做系列答案
相关题目
，
)，且EX=3，DX=1,则P(-1<X<1)=( )
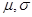)且E(X)=3,D(X)=1,则
= 
=