��Ŀ����
��2012•��������ģ��ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ
��tΪ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У�ԲC�ķ���Ϊ��=2
sin����
������ԲC��ֱ�����귽�̣�
������ԲC��ֱ��l���ڵ�A��B������P������Ϊ��3��
������|PA|+|PB|��
��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ
|
| 5 |
������ԲC��ֱ�����귽�̣�
������ԲC��ֱ��l���ڵ�A��B������P������Ϊ��3��
| 5 |
������������=2
sin������ͬʱ���Ԧѣ��� x=��cos�ȣ�y=��sin�� ����ɵ�ԲC��ֱ�����귽�̣�
����l�IJ������̴���ԲC��ֱ�����귽�̣��� t2-3
t+4=0������ֱ��l�IJ��������в����ļ�������ɵ�|PA|+|PB|=|t1|+|t2|=t1+t2��������һԪ���η��̸���ϵ���Ĺ�ϵ��������
| 5 |
����l�IJ������̴���ԲC��ֱ�����귽�̣��� t2-3
| 2 |
����⣺��������=2
sin�� �� x2+y2-2
y=0 �� x2+(y-
)2=5��
����l�IJ������̴���ԲC��ֱ�����귽�̣��� (3-
t)2+(
t)2=5���� t2-3
t+4=0��
���ڡ�=(3
)2-4��4=2��0���ʿ��� t1��t2���������̵���ʵ��������
��
ֱ��l����P��3��
����������ʽ��t�ļ�������ã�|PA|+|PB|=|t1|+|t2|=t1+t2=3
��
| 5 |
| 5 |
| 5 |
����l�IJ������̴���ԲC��ֱ�����귽�̣��� (3-
| ||
| 2 |
| ||
| 2 |
| 2 |
���ڡ�=(3
| 2 |
|
ֱ��l����P��3��
| 5 |
| 2 |
��������С����Ҫ����ֱ�ߵIJ������̡�Բ�ļ����귽�̡�ֱ����Բ��λ�ù�ϵ�Ȼ���֪ʶ�������������������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
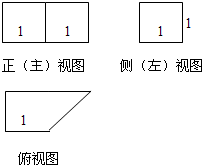 ��2012•��������ģ��һ�������������ͼ��ͼ��ʾ����ü���������Ϊ��������
��2012•��������ģ��һ�������������ͼ��ͼ��ʾ����ü���������Ϊ��������