题目内容
下列三角函数:①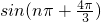 ;②
;②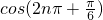 ;③
;③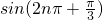 ;④
;④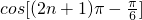 ;⑤
;⑤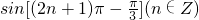 ,其中函数值与
,其中函数值与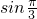 的值相同的是
的值相同的是
- A.①②
- B.①③④
- C.②③⑤
- D.①③⑤
C
分析:①分n为偶数和奇数讨论其值,然后判断是否满足题意;
②利用诱导公式cos(2kπ+α)=cosα化简后,即可判断是否满足题意;
③利用诱导公式sin(2kπ+α)=sinα化简后,即可判断是否满足题意;
④利用诱导公式cos(2kπ+α)=cosα以及cos(π-α)=-cosα化简,即可判断是否满足题意;
⑤利用诱导公式sin(2kπ+α)=cosα以及sin(π-α)=sinα化简,即可判断是否满足题意.
解答:①当n为偶数时,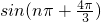 =sin
=sin =sin(π+
=sin(π+ )=-sin
)=-sin ,
,
当n为奇数时,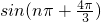 =sin[(n+1)π+
=sin[(n+1)π+ ]=sin
]=sin ,
,
本选项与sin 不同;
不同;
②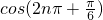 =cos
=cos =cos(
=cos( -
- )=sin
)=sin ,本选项与sin
,本选项与sin 相同;
相同;
③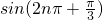 =sin
=sin ,本选项与sin
,本选项与sin 相同;
相同;
④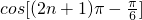 =cos(π-
=cos(π- )=-cos
)=-cos ,本选项与sin
,本选项与sin 不同;
不同;
⑤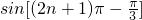 =sin(π-
=sin(π- )=sin
)=sin ,本选项与sin
,本选项与sin 相同,
相同,
则与与sin 相同的序号有②③⑤.
相同的序号有②③⑤.
故选C
点评:此题综合考查了诱导公式的灵活运用.熟记诱导公式是解本题的关键.
分析:①分n为偶数和奇数讨论其值,然后判断是否满足题意;
②利用诱导公式cos(2kπ+α)=cosα化简后,即可判断是否满足题意;
③利用诱导公式sin(2kπ+α)=sinα化简后,即可判断是否满足题意;
④利用诱导公式cos(2kπ+α)=cosα以及cos(π-α)=-cosα化简,即可判断是否满足题意;
⑤利用诱导公式sin(2kπ+α)=cosα以及sin(π-α)=sinα化简,即可判断是否满足题意.
解答:①当n为偶数时,
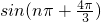 =sin
=sin =sin(π+
=sin(π+ )=-sin
)=-sin ,
,当n为奇数时,
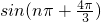 =sin[(n+1)π+
=sin[(n+1)π+ ]=sin
]=sin ,
,本选项与sin
 不同;
不同;②
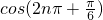 =cos
=cos =cos(
=cos( -
- )=sin
)=sin ,本选项与sin
,本选项与sin 相同;
相同;③
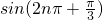 =sin
=sin ,本选项与sin
,本选项与sin 相同;
相同;④
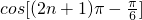 =cos(π-
=cos(π- )=-cos
)=-cos ,本选项与sin
,本选项与sin 不同;
不同;⑤
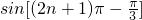 =sin(π-
=sin(π- )=sin
)=sin ,本选项与sin
,本选项与sin 相同,
相同,则与与sin
 相同的序号有②③⑤.
相同的序号有②③⑤.故选C
点评:此题综合考查了诱导公式的灵活运用.熟记诱导公式是解本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目