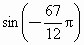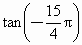题目内容
求下列三角函数值
(1)sin(-1380°)cos1110°+cos(-1020°)sin750°;
(2)2sin
-cos4π+tan(-
).
(1)sin(-1380°)cos1110°+cos(-1020°)sin750°;
(2)2sin
| 5π |
| 4 |
| π |
| 4 |
分析:(1)把所求式子中的角度-1380°变为-360°×4+60°,1110°变为3×360°+30°,-1020°变为-3×360°+60°,750°变为2×360°+30°后,分别利用诱导公式及特殊角的三角函数值化简,即可求出值;
(2)所求式子的第一项中的角5π4变为π+π4,利用诱导公式化简,第二项利用特殊角的三角函数值化简,第三项根据正切函数为奇函数化简,再利用特殊角的三角函数值求出值,把各自求出的值相加即可得到原式的值.
(2)所求式子的第一项中的角5π4变为π+π4,利用诱导公式化简,第二项利用特殊角的三角函数值化简,第三项根据正切函数为奇函数化简,再利用特殊角的三角函数值求出值,把各自求出的值相加即可得到原式的值.
解答:解:(1)sin(-1380°)cos1110°+cos(-1020°)sin750°
=sin(-360°×4+60°)cos(3×360°+30°)+cos(-3×360°+60°)sin(2×360°+30°)
=sin60°cos30°+cos60°sin30°
=sin(60°+30°)
=sin90°
=1;
(2)2sin
-cos4π+tan(-
)
=2sin(π+
)-cos4π-tan
=-2sin
-1-1
=-
-2.
=sin(-360°×4+60°)cos(3×360°+30°)+cos(-3×360°+60°)sin(2×360°+30°)
=sin60°cos30°+cos60°sin30°
=sin(60°+30°)
=sin90°
=1;
(2)2sin
| 5π |
| 4 |
| π |
| 4 |
=2sin(π+
| π |
| 4 |
| π |
| 4 |
=-2sin
| π |
| 4 |
=-
| 2 |
点评:此题考查了诱导公式,正切函数的奇偶性,以及特殊角的三角函数值,熟练掌握诱导公式,灵活变换角度是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
求下列三角函数值
(可用计算器):|
(1) |
(2) |
|
(3)cos398°13′ ; |
(4)tan766°15′ . |