题目内容
(本小题满分12分)
已知数列{ an}的前n项和为Sn,且Sn=2an-l;数列{bn}满足bn-1=bn=bnbn-1(n≥2,n∈N*)b1=1.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求数列 的前n项和T.
的前n项和T.
(Ⅰ)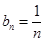 .(Ⅱ)
.(Ⅱ)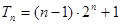 .
.
解析试题分析:(Ⅰ)由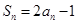 ,得
,得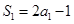 ,所以
,所以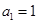 .
.
又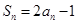 ,
,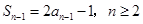 ,
,
两式相减,得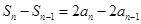 ,
,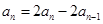 .
.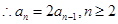 .所以,数列
.所以,数列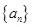 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列. . ……………………………(4分)
. ……………………………(4分)
由 ,得
,得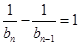 .
.
又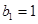 ,所以数列
,所以数列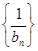 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.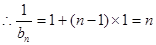 .
.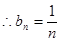 . ……………………………(8分)
. ……………………………(8分)
(Ⅱ)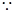
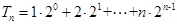 ,
,
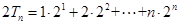 .
.
两式相减,得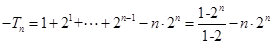
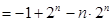 .
.
所以,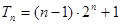 . …………………………(12分)
. …………………………(12分)
考点:本题主要考查等差数列、等比数列的概念,数列的求和。
点评:典型题,“错位相减法”求数列的前n项和属于常考题目,本题解答首先确定数列的通项公式是关键。

练习册系列答案
相关题目
 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前
的前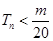 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
 ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。 的前
的前 项和为
项和为 ,且
,且  N
N .
. 是三个互不相等的正整数,且
是三个互不相等的正整数,且 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.  的各项均为正数,
的各项均为正数,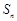 为其前
为其前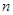 项和,对于任意
项和,对于任意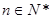 ,总有
,总有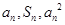 成等差数列.
成等差数列. ,数列
,数列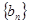 的前
的前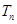 ,求证:
,求证: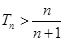 .
. 中,
中, ,
,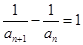 .
.  ,求
,求 的最大值。
的最大值。 ,{bn}的前n项和为Sn,求证
,{bn}的前n项和为Sn,求证

